题目内容
 如图,在直角坐标系中,抛物线与坐标轴分别交于A(0,3),B(
如图,在直角坐标系中,抛物线与坐标轴分别交于A(0,3),B( ,0),C(3
,0),C(3 ,0).
,0).
(1)求该抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切于点E,请判断抛物线的对称轴与⊙C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.
解:(1)设y=ax2+bx+c(a≠0),
将点A(0,3),B( ,0),C(3
,0),C(3 ,0)代入得:
,0)代入得:
 ,
,
解得: ,
,
故二次函数解析式为: ;
;
(2)抛物线的对称轴与⊙C相切;
理由:如图1,过点C作CE⊥BD,垂足为E,
在Rt△OAB中,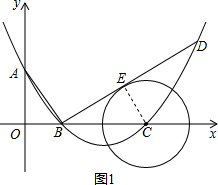
∵OB= ,OA=3,OC=3
,OA=3,OC=3
∴AB=2 ,BC=2
,BC=2 ,
,
∴AB=BC,
又∵∠ABD=90°,
∴∠OBA+∠EBC=90°,
又∵∠OBA+∠OAB=90°,
∴∠OAB=∠EBC,
在△OAB和△EBC中,
 ,
,
∴△OAB≌△EBC(AAS),
∴CE=OB= ;
;
∵抛物线的对称轴为:x=2 ,
,
∴点C到对称轴的距离为: ,
,
∴抛物线的对称轴与⊙C相切;
(3)设AC为y=kx+b′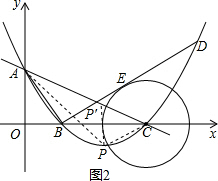
将A(0,3),C(3 ,0)代入得:
,0)代入得:
 ,
,
解得: ,
,
∴AC所在直线解析式为:y=- x+3,
x+3,
如图2,过点P作x轴的垂线,交AC于点P′,连接AP,PC,
则PP′=- x+3-
x+3- x2+
x2+
 x-3
x-3
=- x2+
x2+ x
x
=- (x-
(x- )2+
)2+ ,
,
∴当x= 时,△PAC的面积最大,最大值为:
时,△PAC的面积最大,最大值为: ×PP′×CO=
×PP′×CO=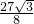 ,
,
当x= 时,y=
时,y= x2-
x2-
 x+3=-
x+3=- ,
,
此时,点P坐标为( ,-
,- ).
).
分析:(1)直接将点A(0,3),B( ,0),C(3
,0),C(3 ,0)代入y=ax2+bx+c,求出a,b,c的值求出即可;
,0)代入y=ax2+bx+c,求出a,b,c的值求出即可;
(2)首先过点C作CE⊥BD,垂足为E,证明△OAB≌△EBC,即可得出CE=OB= ,再利用抛物线的对称轴,即可得出抛物线的对称轴与⊙C的位置关系;
,再利用抛物线的对称轴,即可得出抛物线的对称轴与⊙C的位置关系;
(3)过点P作x轴的垂线,交AC于点P′,首先求出PP′的最值,进而得出,△PAC的面积最大值,进而得出P点坐标.
点评:此题主要考查了待定系数法求二次函数解析式以及待定系数法求一次函数解析式和二次函数最值求法等知识,根据数形结合得出PP′的最值是解题关键.
将点A(0,3),B(
 ,0),C(3
,0),C(3 ,0)代入得:
,0)代入得: ,
,解得:
 ,
,故二次函数解析式为:
 ;
;(2)抛物线的对称轴与⊙C相切;
理由:如图1,过点C作CE⊥BD,垂足为E,
在Rt△OAB中,

∵OB=
 ,OA=3,OC=3
,OA=3,OC=3
∴AB=2
 ,BC=2
,BC=2 ,
,∴AB=BC,
又∵∠ABD=90°,
∴∠OBA+∠EBC=90°,
又∵∠OBA+∠OAB=90°,
∴∠OAB=∠EBC,
在△OAB和△EBC中,
 ,
,∴△OAB≌△EBC(AAS),
∴CE=OB=
 ;
;∵抛物线的对称轴为:x=2
 ,
,∴点C到对称轴的距离为:
 ,
,∴抛物线的对称轴与⊙C相切;
(3)设AC为y=kx+b′

将A(0,3),C(3
 ,0)代入得:
,0)代入得: ,
,解得:
 ,
,∴AC所在直线解析式为:y=-
 x+3,
x+3,如图2,过点P作x轴的垂线,交AC于点P′,连接AP,PC,
则PP′=-
 x+3-
x+3- x2+
x2+
 x-3
x-3=-
 x2+
x2+ x
x=-
 (x-
(x- )2+
)2+ ,
,∴当x=
 时,△PAC的面积最大,最大值为:
时,△PAC的面积最大,最大值为: ×PP′×CO=
×PP′×CO=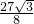 ,
,当x=
 时,y=
时,y= x2-
x2-
 x+3=-
x+3=- ,
,此时,点P坐标为(
 ,-
,- ).
).分析:(1)直接将点A(0,3),B(
 ,0),C(3
,0),C(3 ,0)代入y=ax2+bx+c,求出a,b,c的值求出即可;
,0)代入y=ax2+bx+c,求出a,b,c的值求出即可;(2)首先过点C作CE⊥BD,垂足为E,证明△OAB≌△EBC,即可得出CE=OB=
 ,再利用抛物线的对称轴,即可得出抛物线的对称轴与⊙C的位置关系;
,再利用抛物线的对称轴,即可得出抛物线的对称轴与⊙C的位置关系;(3)过点P作x轴的垂线,交AC于点P′,首先求出PP′的最值,进而得出,△PAC的面积最大值,进而得出P点坐标.
点评:此题主要考查了待定系数法求二次函数解析式以及待定系数法求一次函数解析式和二次函数最值求法等知识,根据数形结合得出PP′的最值是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: