题目内容
 如图所示,小强在华南广场A处观测一楼房顶部安装的广告牌CD,测得广告牌下端D处的仰角为30°,然后前行6m到达B处,又测得该广告牌上端C处的仰角为45°.若B点到楼房的距离BE为30m.求广告牌的高度(
如图所示,小强在华南广场A处观测一楼房顶部安装的广告牌CD,测得广告牌下端D处的仰角为30°,然后前行6m到达B处,又测得该广告牌上端C处的仰角为45°.若B点到楼房的距离BE为30m.求广告牌的高度(| 2 |
| 3 |
分析:根据仰角的定义得到∠CBE=45°,∠DAE=30°,然后在Rt△AED和Rt△BEC中,利用含30°的直角三角形和等腰直角三角形三边的关系分别计算出DE,CE,即可得到CD.
解答:解:在Rt△BEC中,∠E=90°,∠CBE=45°,BE=30,
∴CE=BE=30,
在Rt△AED中,∠E=90°,∠DAE=30°,AE=36,
∴DE=
AE=
×36=12
,
∴CD=CE-DE=30-12
≈9.2.
答:广告牌的高度为9.2m.
∴CE=BE=30,
在Rt△AED中,∠E=90°,∠DAE=30°,AE=36,
∴DE=
| ||
| 3 |
| ||
| 3 |
| 3 |
∴CD=CE-DE=30-12
| 3 |
答:广告牌的高度为9.2m.
点评:本题考查了仰角的概念以及含30°的直角三角形和等腰直角三角形三边的关系.

练习册系列答案
相关题目
 如图所示,小强在华南广场A处观测一楼房顶部安装的广告牌CD,测得广告牌下端D处的仰角为30°,然后前行6m到达B处,又测得该广告牌上端C处的仰角为45°.若B点到楼房的距离BE为30m.求广告牌的高度(
如图所示,小强在华南广场A处观测一楼房顶部安装的广告牌CD,测得广告牌下端D处的仰角为30°,然后前行6m到达B处,又测得该广告牌上端C处的仰角为45°.若B点到楼房的距离BE为30m.求广告牌的高度(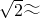 1.41,
1.41, ≈1.73,结果精确到0.1m).
≈1.73,结果精确到0.1m). 1.41,
1.41, ≈1.73,结果精确到0.1m).
≈1.73,结果精确到0.1m).