题目内容
【题目】如图,四边形ABCD中,AD=2AB,∠ABC=90°,将△ABC沿BC翻折得到△A′BC,且A′、C、D三点共线,∠A′CB=52°,则∠CAD=( )
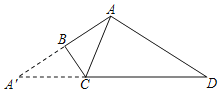
A.78°B.66°C.52°D.38°
【答案】B
【解析】
根据折叠的性质得到A′B=AB,∠ABC=∠A′BC=90°,∠A′CB=∠ACB=52°,从而得出∠A′=∠BAC=38°,∠A′CA=104°,根据等腰三角形的性质得到∠A′=∠D=38°,由三角形的外角的性质即可得到结论.
解:∵∠ABC=90°,将△ABC沿BC翻折得到△A′BC,
∴A′B=AB,∠ABC=∠A′BC=90°,∠A′CB=∠ACB=52°,
∴∠A′=∠BAC=38°,AA′=2AB,∠A′CA=104°
∵AD=2AB,
∴AA′=AD,
∴∠D=∠A′=38°,
∴∠CAD=∠A′CA﹣∠D=104°﹣38°=66°,
故选:B.

练习册系列答案
相关题目
【题目】“三八宏图展,九州春意浓”,为了解某校1000名学生在2017年3月8日“妇女节”期间对母亲表达祝贺的方式,某班兴趣小组随机抽取了部分学生进行问卷调查,并将问卷调查的结果绘制成如下不完整的统计表:
某校抽取学生“妇女节”期间对母亲表达祝贺的方式的统计表
方式 | 频数 | 百分比 |
送母亲礼物 | 23 | 46% |
帮母亲做家务 | ||
给母亲一个爱的拥抱 | 8% | |
其他 | 15 | |
合计 | 100% |
(1)本次问卷调查抽取的学生共有 人,其中通过给母亲一个爱的拥抱表达祝贺的学生有 人.
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示.
(3)根据抽样的结果,估计该校学生通过帮母亲做家务表达祝贺的约有多少人?