题目内容
课题:两个重叠的正多边形,其中的一个绕某一个顶点旋转所形成的有关问题.实验与论证
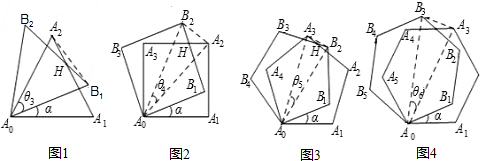
设旋转角∠A1AB1=α(α<∠A1AB1),θ1,θ2,θ3,θ4,θ5,θ6所表示的角如图所示.

(1)用含α的式子表示:θ3=______,θ4=______,θ5=______;θ6=______,
(2)图1中,连接AH时,在不添加其他辅助线的情况下,直线AH是否垂直平分线段A2B1?
答:______;请说明你的理由;
归纳与猜想
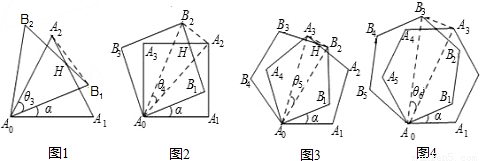
设正n边形AA1A2…An-1与正n边形AB1B2…Bn-1重合(其中,A1与B1重合),现将正n边形AB1B2…Bn-1绕顶点A逆时针旋转α(
 ).
).(3)设θn与上述“θ3,θ4,…”的意义一样,请直接写出θn的度数.
【答案】分析:(1)由正三角形的性质得α+θ3=60°,再由正方形的性质得θ4=45°-(45°-α)=α,最后由正五边形的性质得θ5=108°-36°-36°-α=36°-α;
(2)存在,如在图1中直线AH垂直且平分的线段A2B1,由于△AA1A2与△AB1B2是全等的等边三角形,推得A2H=B1H,则点H在线段A2B1的垂直平分线上;由AA2=AB1,则点A0在线段A2B1的垂直平分线上,从而得出直线AH垂直且平分的线段A2B1
(3)规律:当n为奇数时,θn= -α;当n为偶数时,θn=α.
-α;当n为偶数时,θn=α.
解答: 解:(1)60°-α,α,36°-α.α;
解:(1)60°-α,α,36°-α.α;
(2)是
图1中直线AH垂直平分A2B1,证明如下:
证明:∵△AA1A2与△BB1B2是全等的等边三角形,
∴AA2=AB1,
∴∠AA2B1=∠AB1A2.
又∵△AA1A2与△AB1B2是等边三角形,
∴∠AA2H=∠AB1H=60°.
∴∠HA2B1=∠HB1A2.
∴A2H=B1H.
∴点H在线段A2B1的垂直平分线上.
又∵AA2=AB1,
∴点A在线段A2B1的垂直平分线上.
∴直线AH垂直平分A2B1.
(3)当n为奇数时, ;
;
当n为偶数时,θn=α.
点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.
(2)存在,如在图1中直线AH垂直且平分的线段A2B1,由于△AA1A2与△AB1B2是全等的等边三角形,推得A2H=B1H,则点H在线段A2B1的垂直平分线上;由AA2=AB1,则点A0在线段A2B1的垂直平分线上,从而得出直线AH垂直且平分的线段A2B1
(3)规律:当n为奇数时,θn=
 -α;当n为偶数时,θn=α.
-α;当n为偶数时,θn=α.解答:
 解:(1)60°-α,α,36°-α.α;
解:(1)60°-α,α,36°-α.α;(2)是
图1中直线AH垂直平分A2B1,证明如下:
证明:∵△AA1A2与△BB1B2是全等的等边三角形,
∴AA2=AB1,
∴∠AA2B1=∠AB1A2.
又∵△AA1A2与△AB1B2是等边三角形,
∴∠AA2H=∠AB1H=60°.
∴∠HA2B1=∠HB1A2.
∴A2H=B1H.
∴点H在线段A2B1的垂直平分线上.
又∵AA2=AB1,
∴点A在线段A2B1的垂直平分线上.
∴直线AH垂直平分A2B1.
(3)当n为奇数时,
 ;
; 当n为偶数时,θn=α.
点评:此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
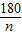 °);
°);
 °);
°);
 °);
°);
 °);
°);