题目内容
如图,已知抛物线 的图象
的图象 ,将其向右平移两个单位后得到图象
,将其向右平移两个单位后得到图象 .
.

(1)求图象 所表示的抛物线的解析式:
所表示的抛物线的解析式:
(2)设抛物线 和
和 轴相交于点
轴相交于点 、点
、点 (点
(点 位于点
位于点 的右侧),顶点为点
的右侧),顶点为点 ,点
,点 位于
位于 轴负半轴上,且到
轴负半轴上,且到 轴的距离等于点
轴的距离等于点 到
到 轴的距离的2倍,求
轴的距离的2倍,求 所在直线的解析式.
所在直线的解析式.
见解析.
【解析】
试题分析:(1)将抛物线y=﹣2x2﹣4x=﹣2(x+1)2+2的图象E,向右平移两个单位后得到图象F,
根据“左加又减,上加下减”规律,所以,图象F所表示的抛物线的解析式为y=﹣2(x+1﹣2)2+2,即y=﹣2(x﹣1)2+2;
(2)由抛物线y=﹣2(x﹣1)2+2,求出顶点C的坐标为(1,2).
令y=0得,﹣2(x﹣1)2+2=0,解得x=0或2,点B的坐标为(2,0).点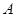 位于
位于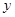 轴负半轴上,所以,设A点坐标为(0,y),则y<0.又因为点A到x轴的距离等于点C到x轴的距离的2倍,即﹣y=2×2,解得y=﹣4,
轴负半轴上,所以,设A点坐标为(0,y),则y<0.又因为点A到x轴的距离等于点C到x轴的距离的2倍,即﹣y=2×2,解得y=﹣4,
所以,A点坐标为(0,﹣4).设AB所在直线的解析式为y=kx+b,把A(0,﹣4),B(2,0)的坐标代入,
解得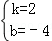 ,写出AB所在直线的解析式为y=2x﹣4.
,写出AB所在直线的解析式为y=2x﹣4.
试题解析:
(1)∵抛物线y=﹣2x2﹣4x=﹣2(x+1)2+2的图象E,将其向右平移两个单位后得到图象F,
∴图象F所表示的抛物线的解析式为y=﹣2(x+1﹣2)2+2,即y=﹣2(x﹣1)2+2;
(2)∵y=﹣2(x﹣1)2+2,
∴顶点C的坐标为(1,2).
当y=0时,﹣2(x﹣1)2+2=0,
解得x=0或2,
∴点B的坐标为(2,0).
设A点坐标为(0,y),则y<0.
∵点A到x轴的距离等于点C到x轴的距离的2倍,
∴﹣y=2×2,解得y=﹣4,
∴A点坐标为(0,﹣4).设AB所在直线的解析式为y=kx+b,
由题意,得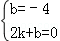 ,
,
解得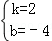 ,
,
∴AB所在直线的解析式为y=2x﹣4.
考点:1.待定系数法求直线的解析式。2. 抛物线的图象和性质

 智能训练练测考系列答案
智能训练练测考系列答案 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA= (2012•黄冈)如图,已知抛物线的方程C1:y=-
(2012•黄冈)如图,已知抛物线的方程C1:y=-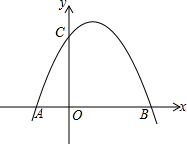 (2013•道外区三模)如图,已知抛物线y=ax2+bx+c过点A(-1,0)、B(3,0)、C(0,3)
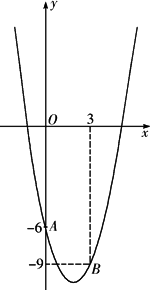
(2013•道外区三模)如图,已知抛物线y=ax2+bx+c过点A(-1,0)、B(3,0)、C(0,3) 如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).
如图,已知抛物线y=ax2-4x+c经过点A(0,-6)和B(3,-9).