题目内容
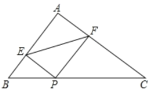
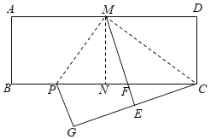
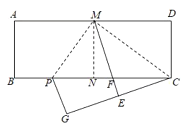
【题目】如图,在矩形ABCD中,AD=2![]() , AB=1.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC=
, AB=1.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G.下列结论:①△CMP是直角三角形;②点C、E、G不在同一条直线上;③PC=![]() MP;④BP=
MP;④BP=![]() ;⑤点F是△CMP外接圆的圆心,其中正确的个数为( )
;⑤点F是△CMP外接圆的圆心,其中正确的个数为( )
A. 2个B. 3个C. 4个D. 5个
【答案】B
【解析】
根据折叠的性质得到∠DMC=∠EMC,∠AMP=∠EMP,于是得到∠PME+∠CME=![]() ×180°=90°,求得△CMP是直角三角形;故①正确;根据平角的定义得到点C、E、G在同一条直线上,故②错误,AB=1,则AD=2
×180°=90°,求得△CMP是直角三角形;故①正确;根据平角的定义得到点C、E、G在同一条直线上,故②错误,AB=1,则AD=2![]() ,得到DM=
,得到DM=![]() AD=
AD=![]() ,根据勾股定理得到CM=
,根据勾股定理得到CM=![]() =
=![]() ,根据射影定理得到CP=
,根据射影定理得到CP=![]() =
=![]() ,得到PC=
,得到PC=![]() MP,故③错误;求得PB=
MP,故③错误;求得PB=![]() AB=
AB=![]() ,故④正确,根据平行线等分线段定理得到CF=PF,求得点F是△CMP外接圆的圆心,故⑤正确.
,故④正确,根据平行线等分线段定理得到CF=PF,求得点F是△CMP外接圆的圆心,故⑤正确.
解:∵沿着CM折叠,点D的对应点为E,
∴∠DMC=∠EMC,
∵再沿着MP折叠,使得AM与EM重合,折痕为MP,
∴∠AMP=∠EMP,
∵∠AMD=180°,
∴∠PME+∠CME=![]() ×180°=90°,
×180°=90°,
∴△CMP是直角三角形;故①正确;
∵沿着CM折叠,点D的对应点为E,
∴∠D=∠MEC=90°,
∵再沿着MP折叠,使得AM与EM重合,折痕为MP,
∴∠MEG=∠A=90°,
∴∠GEC=180°,
∴点C、E、G在同一条直线上,故②错误;
∵AD=2![]() AB,
AB,
∵AB=1,则AD=2![]() ,
,
∵将矩形ABCD对折,得到折痕MN;
∴DM=![]() AD=
AD=![]()
∴CM=![]() =
=![]() ,
,
∵∠PMC=90°,MN⊥PC,
∴CM2=CNCP,
∴CP=![]() =
=![]() ,
,
∴PN=CPCN=![]()
∴PM=![]() =
=![]()
∴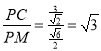 ,
,
∴PC=![]() MP,故③错误;
MP,故③错误;
∵PC=![]() AB=
AB=![]() ,
,
∴PB=![]() -
-![]() =
=![]()
故④正确,
∵CD=CE,EG=AB,AB=CD,
∴CE=EG,
∵∠CEM=∠G=90°,
∴FE∥PG,
∴CF=PF,
∵∠PMC=90°,
∴CF=PF=MF,
∴点F是△CMP外接圆的圆心,故⑤正确;
故选:B.