题目内容
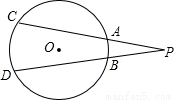
如图，点P是圆O外的一点，直线PAC与圆交A、C两点，直线PBD与圆交于B、D两点．求证：PA•PC=PB•PD．
分析：先连接AB，CD，由圆内接四边形的性质可知∠PAB=∠PDC，∠PBA=∠PCD，故可得出△PAB∽△PDC，再由相似三角形的对应边成比例即可得出结论．
解答：
证明：连接AB，CD，
∵四边形ABDC内接于⊙O，
∴∠PAB=∠PDC，∠PBA=∠PCD，
∴△PAB∽△PDC，
∴
=
，
∴PA•PC=PB•PD．
证明：连接AB，CD，∵四边形ABDC内接于⊙O，
∴∠PAB=∠PDC，∠PBA=∠PCD，
∴△PAB∽△PDC，
∴
| PA |
| PD |
| PB |
| PC |
∴PA•PC=PB•PD．
点评：本题考查的是相似三角形的判定与性质、圆内接四边形的性质，根据题意判断出△PAB∽△PDC是解答此题的关键．
练习册系列答案
相关题目
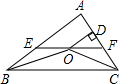如图，点O是△ABC的内心，过点O作EF∥BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC=90°+
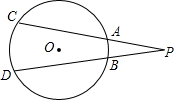如图，点P是圆O外的一点，直线PAC与圆交A、C两点，直线PBD与圆交于B、D两点．