题目内容
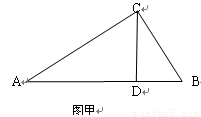
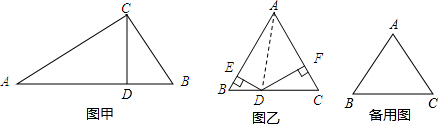
利用“等积”计算或说理是一种很巧妙的方法,就是一个面积从两个不同的角度表示.如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=3,AC=4,求CD的长.
解题思路:利用勾股定理易得AB=5利用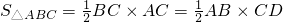 ,可得到CD=2.4
,可得到CD=2.4
请你利用上述方法解答下面问题:
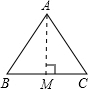
(1)如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=5,AC=12,求CD的长.
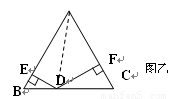
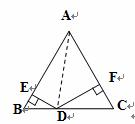
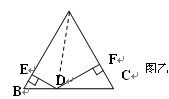
(2)如图乙,△ABC是边长为2的等边三角形,点D是BC边上的任意一点,DE⊥AB于E点,DF⊥AC于F点,求DE+DF的值
分析:①利用备用图计算等边三角形ABC高线的长度
②连接AD,利用S△ABC=S△ADB+S△ADC
解:
 解:(1)∵∠C=90°,BC=5,AC=12,
解:(1)∵∠C=90°,BC=5,AC=12,∴AB=13,
∵S△ABC=
 BC×AC=
BC×AC= AB×CD,
AB×CD,∴5×12=13•CD,
即CD=
 ;
;(2)过点A作AM⊥BC,垂足为M,
∵AB=BC=2,∴BM=1,
∴AM=
 ,
,即等边三角形ABC的高线长是
 …2′,
…2′,由S△ABC=S△ADB+S△ADC得
 BC×
BC× =
= AB×DE+
AB×DE+ AC×DF,
AC×DF,∴
 BC=AB•DE+AC•DF
BC=AB•DE+AC•DF即
 BC=AB•DE+AB•DF
BC=AB•DE+AB•DF∴
 BC=AB(DE+DF),
BC=AB(DE+DF),∵BC=AB=AC,
∴DE+DF=
 …3′.
…3′.分析:(1)先由勾股定理求出AB,再由题干的解题思路得
 BC×AC=
BC×AC= AB×CD,代入数据即可得出CD;
AB×CD,代入数据即可得出CD;(2)根据分析,过点A作AE⊥BC,垂足为E,再根据勾股定理得出AE,由S△ABC=S△ADB+S△ADC求出DE+DF即可.
点评:本题考查了勾股定理、三角形的面积以及等边三角形的性质,是中考的常见题型,要熟练掌握.

练习册系列答案
相关题目
利用“等积”计算或说理是一种很巧妙的方法, 就是一个面积从两个不同的角度表示。如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=3,AC=4,求CD的长。
解题思路:利用勾股定理易得AB=5利用
![]() ,可得到CD=2.4
,可得到CD=2.4
请你利用上述方法解答下面问题:
(1) 如图甲,已知Rt△ABC中,∠C=90°,CD⊥AB于D,BC=5,AC=12,求CD的长。
|

(2)如图乙,△ABC是边长为2的等边三角形,点D是BC边上的任意一点,DE⊥AB于E点,DF⊥AC于F点,求DE+DF的值
|
分析:①利用备用图计算等边三角形ABC高线的长度②连接AD,利用![]()

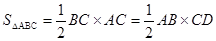 ,可得到CD=2.4
,可得到CD=2.4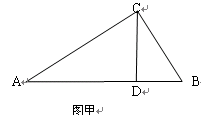
 ,可得到CD=2.4
,可得到CD=2.4