题目内容
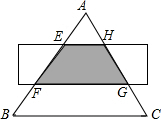如图，△ABC是边长为6cm的等边三角形，被一平行于BC的矩形所截，AB被截成三等分，则图中阴影部分的面积为（ ）| A、4cm2 | ||
B、2
| ||
C、3
| ||
D、4
|
分析：由题意可以推出EH∥FG∥BC，即可知△AEH∽△AFG∽△ABC，结合已知条件便可推出S△AEH：S△AFG：S△ABC=1：4：8，然后求出△ABC的面积，即可推出阴影部分的面积．
解答：
解：过A作AL⊥CB于L，
∵△ABC是边长为6cm的等边三角形，
∴AL=AB•sin60°=6×
=3
（cm），
∴△ABC的面积=
CB•AL=9
cm2，
∵EH∥FG∥BC，
∴△AEH∽△AFG∽△ABC，
∵AB被截成三等分，
∴S△AEH：S△AFG：S△ABC=1：4：9，
∴阴影部分的面积=S△AFG-S△AEH=4
-
=3
cm2．
故选C．
解：过A作AL⊥CB于L，∵△ABC是边长为6cm的等边三角形，
∴AL=AB•sin60°=6×
| ||
| 2 |
| 3 |
∴△ABC的面积=
| 1 |
| 2 |
| 3 |
∵EH∥FG∥BC，
∴△AEH∽△AFG∽△ABC，
∵AB被截成三等分，
∴S△AEH：S△AFG：S△ABC=1：4：9，
∴阴影部分的面积=S△AFG-S△AEH=4
| 3 |
| 3 |
| 3 |
故选C．
点评：本题主要考查相似三角形的判定和性质、等边三角形的性质，关键在于求出S△AEH：S△AFG：S△ABC=1：4：9．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
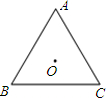如图，△ABC是边长为a的等边三角形，O为△ABC的中心．将△ABC绕着中心O旋转120°．
点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．
（2013•溧水县一模）如图，△ABC是边长为4的等边三角形，将△ABC沿直线BC向右平移，使B点与C点重合，得到△DCE，连结BD，交AC于F．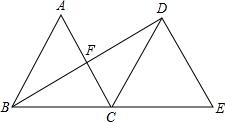
（2012•湘潭）如图，△ABC是边长为3的等边三角形，将△ABC沿直线BC向右平移，使B点与C点重合，得到△DCE，连接BD，交AC于F．
如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，且∠BDC=120°，以D为顶点做一个60°角，使其两边分别交AB于点M，交AC于点N，连接MN，则△AMN的周长为