Question

【题目】如图，已知直线y=-x+2与两坐标轴分别交于A、B两点，⊙C的圆心坐标为（﹣2，0），半径为2，若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积S的取值范围是_____．

Answer 1

【答案】 ≤S≤

【解析】

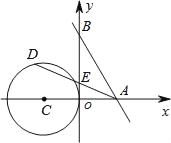
先根据当AD与⊙C相切，且在x轴的上方时，△ABE的面积最小，连接CD，则CD⊥AD，再求出A、B两点的坐标，再根据勾股定理求出AD，从而得出S△ACD，再根据△AOE∽△ADC，求出△ABE的面积，再根据当AD与⊙C相切，且在x轴的下方时，△ABE的面积最大，求出△ABE的面积，即可得出△ABE面积S的取值范围．

解：当AD与⊙C相切，且在x轴的上方时，△ABE的面积最小，

连接CD，则CD⊥AD，

∵直线y=-x+2与两坐标轴分别交于A、B两点，

∴A、B两点的坐标是（2，0），（0，2），

在Rt△ACD中，CD=2，AC=OC+OA=4；

由勾股定理，得：AD=2；

∴S△ACD=ADCD=×2×2=2；

∵△AOE∽△ADC，

∴=（）2=（）2=，

∴S△AOE=S△ADC=；

∴S△ABE=S△AOB-S△AOE=×2×2-=；

当AD与⊙C相切，且在x轴的下方时，△ABE的面积最大，

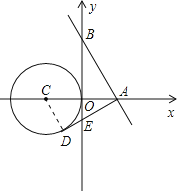
连接CD，则CD⊥AD，

则S△ABE=S△AOB+S△AOE=×2×2+=；

则△ABE面积S的取值范围是 ≤S≤．

故答案为： ≤S≤．