题目内容
（11·柳州）（本题满分10分）如图，直线y＝kx＋k（k≠0）与双曲线
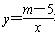在第一象限内相交于点M，与x轴交于点A．（1）求m的取值范围和点A的坐标；
（2）若点B的坐标为（3，0），AM＝5，S△ABM＝8，求双曲线的函数表达式．
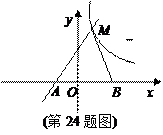
解：（1）∵y＝
在第一象限内
∴m－5＞0
∴m＞5
对直线y＝kx＋k来说
令y＝0
kx＋k＝0 k(x＋1)＝0 ∵k≠0
∴x＋1＝0 x＝－1
点A的坐标（－1，0）
（2）过点M作MC⊥AB于C
∵点A的坐标（－1，0）点B的坐标为（3，0）
∴AB＝4 AO＝1
S△ABM＝
×AB×MC＝×4×MC＝8
∴MC＝4
又∵AM＝5，
∴AC＝3 OA＝1
∴OC＝2
∴点M的坐标（2，4）
把M（2，4）代入y＝得
4＝，则m＝13
∴y＝
解析:
略
在第一象限内∴m－5＞0
∴m＞5
对直线y＝kx＋k来说
令y＝0
kx＋k＝0 k(x＋1)＝0 ∵k≠0
∴x＋1＝0 x＝－1
点A的坐标（－1，0）
（2）过点M作MC⊥AB于C
∵点A的坐标（－1，0）点B的坐标为（3，0）
∴AB＝4 AO＝1S△ABM＝
×AB×MC＝×4×MC＝8∴MC＝4
又∵AM＝5，
∴AC＝3 OA＝1
∴OC＝2
∴点M的坐标（2，4）
把M（2，4）代入y＝
得4＝
，则m＝13∴y＝
解析:略
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
