题目内容
已知:y=ax与y=| b+3 |
| x |
(1)求k的值;
(2)求a、b的值;
(3)如果y=c(c≠0)与函数y=ax和y=
| b+3 |
| x |
| 3 |
| 2 |
分析:(1)由于关于x的一元二次方程有两个不等实根,可用根的判别式及k为非负整数,并满足k≠0确定k的值.
(2)将k值代入求得两不等实根m、n,代入两函数得a、b的值.
(3)先用c表示出A、B两点坐标,由线段AB=
求得c的值.
(2)将k值代入求得两不等实根m、n,代入两函数得a、b的值.
(3)先用c表示出A、B两点坐标,由线段AB=
| 3 |
| 2 |
解答:解:(1)由题意得:△=(2k-7)2-4k(k+3)>0,
解得:k<
.
∵k为非负整数,∴k=0,1.
∵kx2+(2k-7)x+k+3=0为一元二次方程,
∴k=1;
(2)把k=1代入方程得x2-5x+4=0,解得x1=1,x2=4.
∵m<n.
∴m=1,n=4.
把m=1,n=4代入y=ax与y=
可得a=4,b=1;
(3)把y=c代入y=4x与y=
可得:A(
,c)B(
,c),
由AB=
,可得|
-
|=
,
解得c=±2或c=±8,
经检验c1=2,c2=-8为方程的根,
∴c1=2,c2=-8.
解得:k<
| 49 |
| 40 |
∵k为非负整数,∴k=0,1.
∵kx2+(2k-7)x+k+3=0为一元二次方程,
∴k=1;
(2)把k=1代入方程得x2-5x+4=0,解得x1=1,x2=4.
∵m<n.
∴m=1,n=4.
把m=1,n=4代入y=ax与y=
| b+3 |
| x |
(3)把y=c代入y=4x与y=
| 4 |
| x |
| c |
| 4 |
| 4 |
| c |
由AB=
| 3 |
| 2 |
| 4 |
| c |
| c |
| 4 |
| 3 |
| 2 |
解得c=±2或c=±8,
经检验c1=2,c2=-8为方程的根,
∴c1=2,c2=-8.
点评:本题考查了一元二次方程与函数结合的综合应用,由判别式确定一元二次方程是本题的关键.

练习册系列答案
相关题目

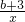 两个函数图象交点为P(m,n),且m<n,m、n是关于x的一元二次方程kx2+(2k-7)x+k+3=0的两个不等实根,其中k为非负整数.
两个函数图象交点为P(m,n),且m<n,m、n是关于x的一元二次方程kx2+(2k-7)x+k+3=0的两个不等实根,其中k为非负整数. ,求c的值.
,求c的值. 相交,如图所示,y1>y2时x的范围是 .
相交,如图所示,y1>y2时x的范围是 .
 两个函数图象交点为P(m,n),且m<n,m、n是关于x的一元二次方程kx2+(2k-7)x+k+3=0的两个不等实根,其中k为非负整数.
两个函数图象交点为P(m,n),且m<n,m、n是关于x的一元二次方程kx2+(2k-7)x+k+3=0的两个不等实根,其中k为非负整数.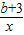 交于A、B两点(点A在点B的左侧),线段AB=
交于A、B两点(点A在点B的左侧),线段AB= ,求c的值.
,求c的值.