题目内容
点A(4,0),B(0,3)与点C构成边长分别为3,4,5的直角三角形,如果点C在反比例函数 的图象上,求k可能取的一切值.
的图象上,求k可能取的一切值.
解:点A和点B之间的距离是5,所以它们之间的连线是直角三角形的斜边.设点C的坐标为(a,b),
则 ①,或者
①,或者 ②,
②,
对于①,有 ,
,
两式相减得:8a-6b-14=0,
因此b= (4a-7),
(4a-7),
将它代入①中的第二个式子,得: ,
,
解得 a=4,或a=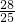 ,
,
对应 b的值是 3或 ,
,
所以点C的坐标是(4,3)或(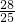 ,
, ).
).
对应的k 的值是12或 .
.
对于.②,有 ,
,
两式相减,得 8a-6b=0.
因此,b= a.
a.
将它代入(2)的第一个式子,得
 a(25a-72)=0.
a(25a-72)=0.
解得 a=0或a= ,
,
对应的b的值是0或 .
.
因为原点不可能在反比例函数的图象上,所以点C的坐标是( ,
, ),对应的k的值是
),对应的k的值是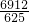 .
.
综上所述,k的值是12或 或
或 .
.
分析:根据题目中的条件知:点A与点B的连线是直角三角形的斜边,设出点C的坐标,根据以上条件列出关于a、b的方程组将点C的坐标求出来即可.
点评:本题考查了反比例函数的知识,但在本题中出现了二元二次方程组的知识,学生在应用时往往会出现缩手缩脚的现象,其实在解题时能转化为普通的二元一次方程组来解.
则
 ①,或者
①,或者 ②,
②,对于①,有
 ,
,两式相减得:8a-6b-14=0,
因此b=
 (4a-7),
(4a-7),将它代入①中的第二个式子,得:
 ,
,解得 a=4,或a=
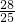 ,
,对应 b的值是 3或
 ,
,所以点C的坐标是(4,3)或(
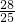 ,
, ).
).对应的k 的值是12或
 .
.对于.②,有
 ,
,两式相减,得 8a-6b=0.
因此,b=
 a.
a.将它代入(2)的第一个式子,得
 a(25a-72)=0.
a(25a-72)=0.解得 a=0或a=
 ,
,对应的b的值是0或
 .
.因为原点不可能在反比例函数的图象上,所以点C的坐标是(
 ,
, ),对应的k的值是
),对应的k的值是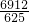 .
.综上所述,k的值是12或
 或
或 .
.分析:根据题目中的条件知:点A与点B的连线是直角三角形的斜边,设出点C的坐标,根据以上条件列出关于a、b的方程组将点C的坐标求出来即可.
点评:本题考查了反比例函数的知识,但在本题中出现了二元二次方程组的知识,学生在应用时往往会出现缩手缩脚的现象,其实在解题时能转化为普通的二元一次方程组来解.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
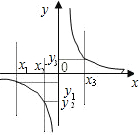 在函数y=
在函数y=| k |
| x |
| A、y1<0<y2 |
| B、y3<0<y1 |
| C、y2<y1<y3 |
| D、y3<y1<y2 |
 9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为
9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为 23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.