��Ŀ����
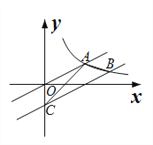
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��2��3����B��6��3��������AB���������ƽ����һ��P���߶�AB�϶����ڵ�Q��ʹ��PQ��1����ô�Ƶ�P���߶�AB��������������
��1�����жϵ�D��4.5��2.5���Ƿ����߶�AB��������������
��2�������H ��m��n����һ�κ���![]() ��ͼ���ϣ������߶�AB����������������m��ȡֵ��Χ��
��ͼ���ϣ������߶�AB����������������m��ȡֵ��Χ��
��3�����һ�κ���y=x+b��ͼ�������ٴ���һ����������������ֱ��д��b��ȡֵ��Χ��
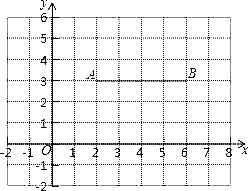
���𰸡���1����D��4.5��2.5�����߶�AB�ġ������㡱��
��2��m��ȡֵ��Χ��![]() ��
��
��3��b��ȡֵ��Χ��![]()
��������
��1����P���߶�AB�ġ������㡱�Ķ��弴���ж�.
��2���������ֱ��y=![]() x-2���߶�AB���ڣ�
x-2���߶�AB���ڣ�![]() ��3���֢ٵ�m��
��3���֢ٵ�m��![]() ʱ���г�����ʽ���ɽ������.
ʱ���г�����ʽ���ɽ������.
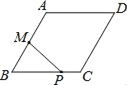
��3����ͼ����Rt��AMN�У�AM=1����MAN=45�㣬���M���꣨2-![]() ��3+
��3+![]() ������Rt��BEF�У�BE=1����EBF=45�㣬���E���꣨6+
������Rt��BEF�У�BE=1����EBF=45�㣬���E���꣨6+![]() ��3-
��3-![]() ����
����
�ֱ����ֱ�߾�����M��Eʱ��b��ֵ�����ɽ������.
�⣺��1���ߵ�D���߶�AB�ľ�����0.5��
��0.5<1��
���D��4.5��2.5���Ƿ����߶�AB�ġ������㡱��
��2���ߵ�H��m��n���߶�AB�ġ����ӵ㡱����H��m��n����ֱ��y=![]() x-2�ϣ�
x-2�ϣ�
��n=![]() m-2��
m-2��
ֱ��y=![]() x-2
x-2![]() �߶�AB���ڣ�
�߶�AB���ڣ�![]() ��3��.
��3��.
�ٵ�m��![]() ʱ����n=
ʱ����n=![]() m-2��3��
m-2��3��
��AB��x�ᣬ���ʱ��H��m��n�����߶�AB�ľ�����n-3.
��0��n-3����![]() ��m��5.
��m��5.
����������![]() ��m��5.
��m��5.
��3����ͼ����Rt��AMN�У�AM=1����MAN=45�㣬���M���꣨2-![]() ��3+
��3+![]() ����
����

��Rt��BEF�У�BE=1����ENF=45�㣬���E���꣨6+![]() ��3-
��3-![]() ����
����
��ֱ��y=x+b������Mʱ��b=1+![]() ����ֱ��y=x+b������Eʱ��b=-3-
����ֱ��y=x+b������Eʱ��b=-3-![]() ��
��
��-3-![]() ��b��1+
��b��1+![]() .
.
���㾦�����⿼��һ�κ����ۺ��⡢�߶�AB�ġ������㡱�Ķ����֪ʶ������Ĺؼ����������⣬ѧ��������ۣ�ѧ����������������⣬�����е�ѹ����.