题目内容
已知△ABC中，AC=3cm，BC=4cm，AB=5cm，则△ABC的外接圆半径是（ ）
| A、2cm | B、2.5cm | C、3cm | D、4cm |
分析：因为△ABC三边长分别为3cm、4cm、5cm，符合勾股定理，即△ABC是直角三角形；由直角三角形的特征知，圆心为斜边中点，半径等于斜边的一半．
解答：解：∵32+42=52，
∴△ABC是直角三角形，且AB为斜边，
∴三角形外接圆的半径=
×5=2.5cm，
∴三角形外接圆的半径等于2.5cm．
故选B．
∴△ABC是直角三角形，且AB为斜边，
∴三角形外接圆的半径=
| 1 |
| 2 |
∴三角形外接圆的半径等于2.5cm．
故选B．
点评：本题考查的是直角三角形的外接圆半径，重点在于理解直角三角形的外接圆是以斜边中点为圆心，斜边长的一半为半径的圆．
练习册系列答案
相关题目
12、已知△ABC中，AC=BC，∠C=Rt∠．如图，将△ABC进行折叠，使点A落在线段BC上（包括点B和点C），设点A的落点为D，折痕为EF，当△DEF是等腰三角形时，点D可能的位置共有（ ）
如图：已知△ABC中，AC=BC，∠ACB=90°，直角∠DFE的顶点F是AB中点，两边FD、FE分别交AC，BC于点D，E两点，给出以下个结论：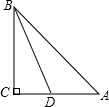
如图，已知△ABC中，AC=BC，∠ACB=90°，BD平分∠ABC，求证：AB=BC+CD．
已知△ABC中，AC=BC，AD平分∠BAC交BC于D，点E为AB上一点，且∠EDB=∠B，现有下列两个结论：①AB=AD+CD ②AB=AC+CD．