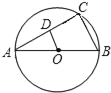
题目内容
【题目】如图,点A在函数y=![]() (x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=
(x>0)图象上,过点A作x轴和y轴的平行线分别交函数y=![]() 图象于点B,C,直线BC与坐标轴的交点为D,E.
图象于点B,C,直线BC与坐标轴的交点为D,E.
(1)当点C的横坐标为1时,求点B的坐标;
(2)试问:当点A在函数y=![]() (x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(x>0)图象上运动时,△ABC的面积是否发生变化?若不变,请求出△ABC的面积,若变化,请说明理由.
(3)试说明:当点A在函数y=![]() (x>0)图象上运动时,线段BD与CE的长始终相等.
(x>0)图象上运动时,线段BD与CE的长始终相等.
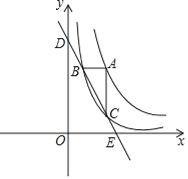
【答案】(1)B点坐标为(![]() ,4);
,4);
(2)即△ABC的面积不发生变化,其面积为![]() ;
;
(3)证明见解析.
【解析】试题分析:(1)由条件可先求得A点坐标,从而可求得B点纵坐标,再代入y=![]() 可求得B点坐标;
可求得B点坐标;
(2)可设出A点坐标,从而可表示出C、B的坐标,则可表示出AB和AC的长,可求得△ABC的面积;
(3)可证明△ABC∽△EFC,利用(2)中,AB和AC的长可表示出EF,可得到BG=EF,从而可证明△DBG≌△CFE,可得到DB=CF.
解析:(1)∵点C在y=![]() 的图象上,且C点横坐标为1,
的图象上,且C点横坐标为1,
∴C(1,1),
∵AC∥y轴,AB∥x轴,
∴A点横坐标为1,
∵A点在函数y=![]() (x>0)图象上,
(x>0)图象上,
∴A(1,4),
∴B点纵坐标为4,
∵点B在y=![]() 的图象上,
的图象上,
∴B点坐标为(![]() ,4);
,4);
(2)设A(a,![]() ),则C(a,
),则C(a,![]() ),B(
),B(![]() ,
,![]() ),
),
∴AB=a﹣![]() =
=![]() a,AC=
a,AC=![]() ﹣
﹣![]() =
=![]() ,
,
∴S△ABC=![]() ABAC=
ABAC=![]() ,
,
即△ABC的面积不发生变化,其面积为![]() ;
;
(3)如图,设AB的延长线交y轴于点G,AC的延长线交x轴于点F,
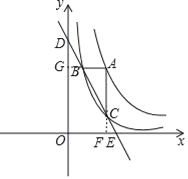
∵AB∥x轴,
∴△ABC∽△EFC,
∴![]() ,即
,即![]() ,
,
∴EF=![]() a,
a,
由(2)可知BG=![]() a,
a,
∴BG=EF,
∵AE∥y轴,∴∠BDG=∠FCE,
在△DBG和△CFE中
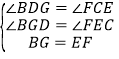
∴△DBG≌△CEF(AAS),
∴BD=EF.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目