题目内容
2. 多边形的内角和与外角和
多边形的内角和与外角和多边形的内角和是(n-2)•180°;多边形的外角和是360°.
(1)若一个多边形的内角和是1440°,则这个多边形的边数是10.
(2)如图:∠A+∠B+∠C+∠D+∠E+∠F=360°.
分析 根据多边形的内角和公式即可求解;根据多边形的外角和定理即可求解.
(1)根据多边形的内角和公式即可求解;
(2)根据三角形外角的性质和多边形的外角和定理即可求解.
解答 解:多边形的内角和是(n-2)•180°;多边形的外角和是360°.
(1)1440÷180+2=10.
故这个多边形的边数是 10.
(2)如图: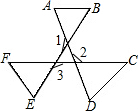
∠A+∠B+∠C+∠D+∠E+∠F=(∠A+∠B)+(∠C+∠D)+(∠E+∠F)=∠1+∠2+∠3=360°.
故答案为:(n-2)•180°;360°.(1)10;(2)360°.
点评 考查了多边形内角与外角,关键是熟悉多边形内角和定理:(n-2)•180° (n≥3)且n为整数),同时涉及三角形的性质和三角形的外角和等于360度的知识点.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
17.如果两条不同的直线都和第三条直线平行,那么这两条直线的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 互相垂直 |
11.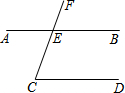 如图,已知AB∥CD,CF交AB于点E,∠AEF=102°36′,则∠C等于( )
如图,已知AB∥CD,CF交AB于点E,∠AEF=102°36′,则∠C等于( )
 如图,已知AB∥CD,CF交AB于点E,∠AEF=102°36′,则∠C等于( )
如图,已知AB∥CD,CF交AB于点E,∠AEF=102°36′,则∠C等于( )| A. | 77°24′ | B. | 78°24′ | C. | 78°36′ | D. | 102°36′ |
12.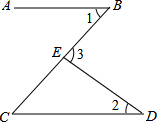 如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
 如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )| A. | 80° | B. | 70° | C. | 90° | D. | 100° |
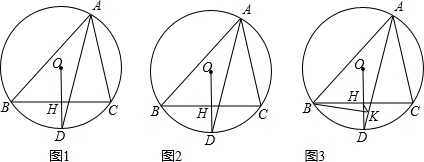
 将△ABC沿BC方向平移,使点B移到点C
将△ABC沿BC方向平移,使点B移到点C