题目内容
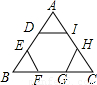
如图，正六边形ABCDEF的边长为1，连接AE、BD、CF，则图中灰色四边形的周长为________．
2+
分析：根据正六边形的性质得出BC=1=CD=GH，CG=
=HD，进而得出四边形CDHG的周长．
解答：
解：如图：
∵ABCDEF为正六边形，
∴∠ABC=120°，∠CBG=60°，
又∵BC=1=CD=GH，
∴CG==HD，
∴四边形CDHG的周长=（1+）×2=2+．
故答案为：2+．
点评：本题主要考查的是正多边形和圆，先根据已知得出GH=1以及CG的长是解题关键．
分析：根据正六边形的性质得出BC=1=CD=GH，CG=
=HD，进而得出四边形CDHG的周长．解答：
解：如图：∵ABCDEF为正六边形，
∴∠ABC=120°，∠CBG=60°，
又∵BC=1=CD=GH，
∴CG=
=HD，∴四边形CDHG的周长=（1+
）×2=2+．故答案为：2+
．点评：本题主要考查的是正多边形和圆，先根据已知得出GH=1以及CG的长是解题关键．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
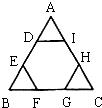18、如图，正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上，则这个正六边形的边长是
