Question

【题目】已知一次函数图象经过（6，）、（2，）两点.

(1)求函数解析式；

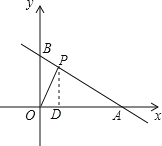
(2)该函数图象与x、y轴分别交于A、B两点，点P是该函数图象第一象限内的一点，当△OAP的面积为12时，求点P的坐标.

Answer 1

【答案】（1）；（2）P(4,3).

【解析】

（1）直接利用待定系数法求解即可；

（2）根据三角形的面积公式S△OPAOAy，然后把y转换成x，△OPA的面积S与x的函数关系式就可以求出了，再把S=12代入的解析式里．就可以求出x，然后确定P的坐标．

（1）设函数解析式为：y=kx+b，则有：

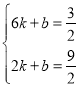
解得：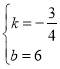

∴该函数解式为：；

（2）∵点P（x，y）在第一象限内的直线yx+6上，∴点P的坐标为（x，x+6）且x＞0，x+6＞0．

过点P作PD⊥x轴于点D，则△OPA的面积OA×PD，即S8×（x+6），∴S=﹣3x+24=12，解得：x=4，把x=4代入yx+6，得y=3，这时，P的坐标为（4，3）；

即当P运动到点（4，3）这个位置时，△OPA的面积为12．