题目内容
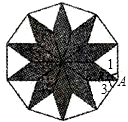 右边的图案是由两种多边形密铺而成的正十边形,在拼接点A处,∠3的度数是
右边的图案是由两种多边形密铺而成的正十边形,在拼接点A处,∠3的度数是
- A.36°
- B.45°
- C.54°
- D.60°
C
分析:先计算出正十边形的中心角= =36°,正十边形的每个内角=180°-
=36°,正十边形的每个内角=180°- =144°,然后由∠1+∠3+36°=144°即可得到∠3.
=144°,然后由∠1+∠3+36°=144°即可得到∠3.
解答:∵正十边形的中心角= =36°,正十边形的每个内角=180°-
=36°,正十边形的每个内角=180°- =144°,
=144°,
∴∠1+∠3+36°=144°,
∴∠3=108°÷2=54°.
故答案为54°.
点评:本题考查了多边形内角和定理和外角和定理:多边形内角和为(n-2)•180°,外角和为360°.
分析:先计算出正十边形的中心角=
 =36°,正十边形的每个内角=180°-
=36°,正十边形的每个内角=180°- =144°,然后由∠1+∠3+36°=144°即可得到∠3.
=144°,然后由∠1+∠3+36°=144°即可得到∠3.解答:∵正十边形的中心角=
 =36°,正十边形的每个内角=180°-
=36°,正十边形的每个内角=180°- =144°,
=144°,∴∠1+∠3+36°=144°,
∴∠3=108°÷2=54°.
故答案为54°.
点评:本题考查了多边形内角和定理和外角和定理:多边形内角和为(n-2)•180°,外角和为360°.

练习册系列答案
相关题目
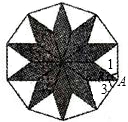 右边的图案是由两种多边形密铺而成的正十边形,在拼接点A处,∠3的度数是( )
右边的图案是由两种多边形密铺而成的正十边形,在拼接点A处,∠3的度数是( )| A、36° | B、45° | C、54° | D、60° |
 20、如图的图案是由几种正多边形密铺而成的,在拼接点A处,各角的度数是
20、如图的图案是由几种正多边形密铺而成的,在拼接点A处,各角的度数是
