题目内容
【题目】如图，直线
图像与y轴、x轴分别交于A、B两点
（1）求点A、B坐标和∠BAO度数
（2）点C、D分别是线段OA、AB上一动点（不与端点重合），且CD=DA，设线段OC的长度为x ,
,请求出y关于x的函数关系式以及定义域
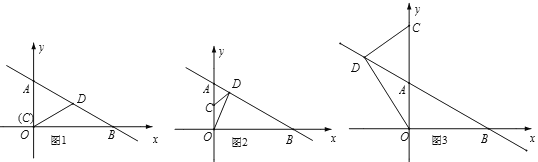
（3）点C、D分别是射线OA、射线BA上一动点，且CD=DA，当ΔODB为等腰三角形时，求C的坐标（第（3）小题直接写出分类情况和答案，不用过程）
【答案】（1）A(0,3),B(
),60°（2）
（0＜x＜3）（3）（0，0），
，（0，6）
【解析】
(1)对于一次函数解析式，分别令x与y为0求出对应的y与x的值，得到A、B两点坐标，然后再根据三角函数求出∠BAO的度数即可；
(2)先证明△ACD是等边三角形，根据等边三角形的性质可得AD=CD=AC=3-x，作DH⊥y轴于点H，用含x的式子表示出DH的长，然后根据三角形面积公式进行求解即可；
(3)当△ODB为等腰三角形时，分三种情况讨论：当OD=DB时；当BD=BO时；当OD=OB时，利用等边三角形的性质分别求出C点坐标即可.
(1)一次函数
，
令
，则有
，解得：
，
，
令
，得
，
，
，
在
，
，
∵sin∠ABO=
，
，
；
(2)过点D作DH⊥y轴，垂足为点H，
，
，
，
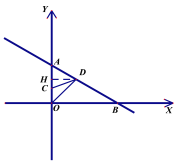
∴ΔADC是等边三角形，
，
，
=
=
，
∵S△OCD=
，
；
(3)由(1)知，在Rt△OAB中，OA=3，OB=3
，∠BAO=60°，AB=6，∠ABO=30°，
当△ODB为等腰三角形时，分三种情况进行讨论：
①如图1，当OD=DB时，D在OB的垂直平分线上，则D为AB的中点，AD=
AB=3，
∵CD=DA，∠CAD=60°，
∴△ACD是等边三角形，
∴AC=AD=3，
∴C与原点重合，
∴C点坐标为(0，0)；
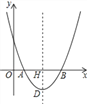
②如图2，当BD=BO=3时，AD=AB-BD=6-3，
∵CD=DA，∠CAD=60°，
∴△ACD是等边三角形，
∴AC=AD=6-3，
∴OC=OA-AC=3-(6-3)=3-3，
∴C点坐标为(0，3-3)；
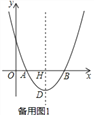
③如图3，当OD=OB=3时，∠ODB=∠OBD=30°，
∵∠AOD=∠BAO-∠ODB=60°-30°，
∴∠ODB=∠AOD=30°，
∴AD=OA=3，
∵CD=DA，∠CAD=60°，
∴△ACD是等边三角形，
∴AC=AD=3，
∴OC=OA+AC=3+3=6，
∴C点坐标为(0，6)，
综上，点C的坐标为(0，0)，
，(0，6).
