Question

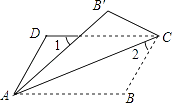
【题目】如图，在四边形ABCD中，AD∥BC，AB=BC=6，∠B=60°，∠D=90°，连结AC．动点P从点B出发，沿BC以每秒1个单位的速度向终点C运动（点P不与点B、C重合）．过点P作PQ⊥BC交AB或AC于点Q，以PQ为斜边作Rt△PQR，使PR∥AB．设点P的运动时间为t秒．

（1）当点Q在线段AB上时，求线段PQ的长．（用含t的代数式表示）
（2）当点R落在线段AC上时，求t的值．
（3）设△PQR与△ABC重叠部分图形的面积为S平方单位，求S与t之间的函数关系式．
（4）当点R到C、D两点的距离相等时，直接写出t的值．

Answer 1

【答案】
（1）解：如图1中，

当点Q在线段AB上时，BP=t，

在Rt△PQB中，∵∠BPQ=90°，∠B=60°，

∴PQ=BPtan60°= t（0＜t≤3）

（2）解：如图2中，

当R落在AC上时，易知PC=RC=PQ，

在Rt△PQR中，∵∠PRQ=90°，PQ= t，∠PQR=60°，

∴PR=PQsin60°= t，

由BP+PC=6可得，t+ t=6，

解得t= s

（3）解：如图3中．当0＜t≤ 时，重叠部分是△PQR．

S= QRPR= t t= t2．

如图4中，当 ＜t≤3时，重叠部分是四边形PMNQ．

S=S△PQR﹣S△RMN= t2﹣ [ t﹣（6﹣t）] [ t﹣（6﹣t）]=﹣ t2+15 t﹣18 ．

如图5中，当3＜t＜6时，重叠部分是△PQM．

S= S△PQC= （6﹣t） （6﹣t）= t2﹣3 t+9

（4）解：在图3中，点R到C、D两点的距离相等时，则有 tsin60°= ×6× ，解得t=2．

在图5中，点R到C、D两点的距离相等时，则有 （6﹣t） = 6 ，解得t=4．

综上所述，t=2s或4s时，点R到C、D两点的距离相等

【解析】（1）Rt△PQB中利用解直角三角形易求出线段PQ的长。
（2）当R落在AC上时，易知PC=RC=PQ，在Rt△PQR中，利用解直角三角形求出PR= 3 2 t，由BP+PC=6，建立方程求出t的值。
（3）分三种情况进行讨论：如图3中．当0＜t≤ 时，重叠部分是△PQR．根据三角形的面积公式，可求出S与t之间的函数关系式；如图4中，当 ＜t≤3时，重叠部分是四边形PMNQ，根据S=S△PQR﹣S△RMN即可求出结果；如图5中，当3＜t＜6时，重叠部分是△PQM．则S= S△PQC，即可求出S与t之间的函数关系式。
（4）根据两种情况在图3和图5中，根据点R到C、D两点的距离相等建立方程求解即可。
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．