Question

（2013•海门市一模）如图，直线l的解析式为y=-

4

3

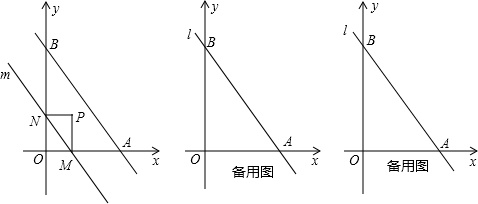
x+4，它与x轴、y轴分别相交于A、B两点，平行于直线l的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，它与x轴、y轴分别相交于M、N两点，运动时间为t秒（0＜t≤3）
（1）求A、B两点的坐标；
（2）以MN为对角线作矩形OMPN，记△MPN和△OAB重合部分的面积为S，试探究S与t之间的函数关系；
（3）当S=2时，是否存在点R，使△RNM∽△AOB？若存在，求出R的坐标；若不存在，请说明理由．

Answer 1

分析：（1）由直线的解析式，分别让x、y为0，可求得A、B的坐标；
（2）分两类情况进行讨论，Ⅰ当点P在直线AB左边时，分别用t表示出PM、PN，然后根据三角形面积公式求出s与t的关系式，当点P在直线AB右边时，同理求出s与t的关系式；
（3）分别令s₁=

2

3

t²，s₂=-2t²+8t-6=2，求出满足条件的t的值，进而求出M和N的坐标，再根据△RNM∽△AOB求出点R的坐标．

解答：解：（1）当y=0时，0=-

4

3

x+4
解得x=3，
即A（3，0），
当x=0时，y=4
即B（0，4）；

（2）Ⅰ当点P在直线AB左边时，
∵矩形OMPN，
∴NP=OM=t
∵m∥l
∴△OMN∽△OAB
∴

OM

OA

=

ON

OB

，
∴

t

3

=

ON

4

，
∴PM=ON=

4

3

t，
∴s₁=

1

2

PN•PM=

1

2

•t•

4

3

t=

2

3

t²（0＜t≤

3

2

），

Ⅱ当点P在直线AB右边时，
∵OM=t，
∴AM=3-t，
∴ME=

4

3

（3-t），
PE=

4

3

t-

4

3

（3-t）=

8

3

t-4，
PF=

3

4

-（

8

3

t-4）=2t-3，
∴s₂=

1

2

PN•PM-

1

2

PE•PF，
=

1

2

t•

4

3

t-

1

2

（

8

3

t-4）（2t-3）=-2t²+8t-6（

3

2

＜t≤3），
综上所述：s₁=

2

3

t²（0＜t≤

3

2

），或s₂=-2t²+8t-6（

3

2

＜t≤3）；

（3）当s₁=

2

3

t²=2时，t=

3

＞

3

2

，舍去，
当s₂=-2t²+8t-6=2时，t₁=t₂=2，
此时M（2，0），N（0，

8

3

），
∴存在R₁和R₂使△RNM∽△AOB，
∴∠RNM=∠AOB=90°，∠R₁MN=∠ABO=∠MNO，
∴R₁M∥y轴，
∴R₁H₁=OM=2，
∴NH₁=2×

3

4

=

3

2

，
∴OH₁=

8

3

+

3

2

=

25

6

，
∴R₁（2，

25

6

），
∴R₂H₂=R₁H₁=2，NH₂=NH₁=

3

2

，
∴OH₂=

8

3

-

3

2

=

7

6

，
∴R₂（-2，

7

6

），
综上所述：R₁（2，

25

6

）或R₂（-2，

7

6

）．

点评：本题主要考查了一次函数综合题的知识点，熟练掌握函数图象与坐标轴的交点的求法，以及利用三角形的相似的性质，本题是一个难度较大的综合题．