题目内容
如图,AD是⊙O的直径,过⊙O上一点E作直线l,交AD的延长线如点B,AC⊥l于点C,AC交 ⊙O于点G,E为
⊙O于点G,E为 的中点.
的中点.
(1)求证:BC是⊙O的切线;
(2)若AC+GC=5,⊙O的半径为r,求代数式 +
+ 的值.
的值.
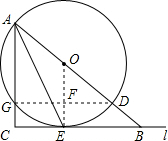 (1)证明:连接OE,GD交于F.
(1)证明:连接OE,GD交于F.∵AD是⊙O的直径,
∴OE=OA,
∴∠OEA=∠OAE,
∵E为
 的中点,∴
的中点,∴ =
= ,
,∴∠GAE=∠OAE,
∴∠OEA=∠GAE,
∴OE∥AC,
又AC⊥BC,
∴BC是⊙O的切线;
(2)解:∵OE∥AC,OD=OA,
∴OF三角形AGD的中位线,
∴OF=r-EF=
 (AC-CG)=
(AC-CG)= (AC+GC-2GC)=
(AC+GC-2GC)= ×5-GC=
×5-GC= -GC,
-GC,则r=
 .
.把r=
 代入代数式
代入代数式 +
+ 得:
得: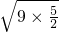 +
+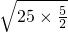 =4
=4 ,
,所以代数式
 +
+ 的值为4
的值为4 .
.分析:(1)连接OE,OE=OA,则得∠OEA=∠OAE,又由,E为
 的中点,推出
的中点,推出 =
= ,所以∠GAE=∠OAE,则∠OEA=∠GAE,所以OE∥AC,因此OE⊥BC,从而证得BC是⊙O的切线;
,所以∠GAE=∠OAE,则∠OEA=∠GAE,所以OE∥AC,因此OE⊥BC,从而证得BC是⊙O的切线;(2)由(1)证得OE∥AC,OD=OA,所以OF是三角形ADG的中位线,所以可求出r,从而求出代数式
 +
+ 的值.
的值.点评:此题考查的知识点是切线的判定、等腰三角形的判定与性质,关键(1)是先由半径的等腰三角形得角相等,等弧的圆周角相等,得OE∥AC,即得AC⊥BC,从而得证;(2)关键是先证得OF是三角形AGD的中位线,从而求出半径r.

练习册系列答案
相关题目
 0.1平方米)
0.1平方米) 如图,某水库堤坝的横断面为梯形,背水坡AD的坡比(坡比是斜坡的铅直距离与水平距离的比)为1:1.5,迎水坡BC的坡比为1:
如图,某水库堤坝的横断面为梯形,背水坡AD的坡比(坡比是斜坡的铅直距离与水平距离的比)为1:1.5,迎水坡BC的坡比为1: 某市的跨江斜拉大桥建成通车,如图,BC是水平桥面,AD是竖直桥墩,按工程设计的要求,斜拉的钢线AB、AC应相等,请你用学过的知识来检验AB、AC的长度是相等的,写出你的检验方法步骤,并简要说明理由.(检验工具为刻度尺、测角仪;检验时,人只能站在桥面上)
某市的跨江斜拉大桥建成通车,如图,BC是水平桥面,AD是竖直桥墩,按工程设计的要求,斜拉的钢线AB、AC应相等,请你用学过的知识来检验AB、AC的长度是相等的,写出你的检验方法步骤,并简要说明理由.(检验工具为刻度尺、测角仪;检验时,人只能站在桥面上) 0.1平方米)
0.1平方米)