题目内容
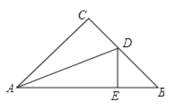
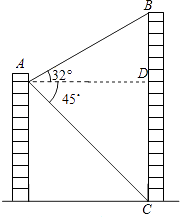
【题目】如图,若四边形ABCD、四边形GFED都是正方形,AD=4, ![]() ,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 .
,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 . 
【答案】![]()
【解析】解:过点E作EQ⊥CD于Q,则∠EQD=90°,
∵正方形DEFG中∠EDF=45°,正方形ABCD中∠ADC=90°,
∴∠EDQ=90°﹣45°=45°,
∴△DEQ是等腰直角三角形,
∵DE= ![]() ,
,
∴EQ=DQ=1,
又∵AD=4=CD,
∴CQ=4﹣1=3,
∵EQ∥MD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DM= ![]() ,
,
∴直角三角形CDM中,CM= ![]() =
= ![]() .
.
所以答案是: ![]()

【考点精析】利用正方形的性质和旋转的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目