题目内容
【题目】已知△ABC中,∠ABC=90°,将△ABC绕点B逆时针旋转90°后,点A的对应点为点D,点C的对应点为点E,直线DE与直线AC交于点F,连接FB.
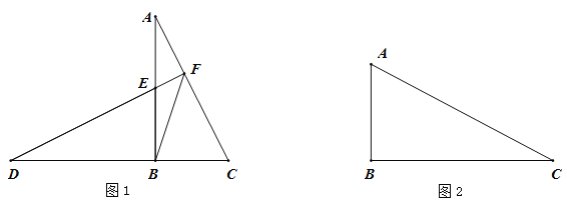
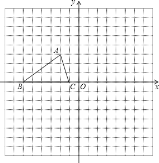
(1)如图1,当∠BAC<45°时,
①求证:DF⊥AC;
②求∠DFB的度数;
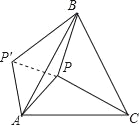
(2)如图2,当∠BAC>45°时,
①请依题意补全图2;
②用等式表示线段FC,FB,FE之间的数量关系,并证明.
【答案】(1)①详见解析;②45°;(2)①见解析②FC-FE=![]() FB
FB
【解析】
(1)①根据旋转的性质可得△ABC≌△DBE,再根据全等三角形的性质和直角三角形的性质即可证明;
②证法一:先证明A,D,B,F四点均在以AB为直径的圆上,再连接AD,证明△ABD是等腰直角三角形即可;证法二:在DE上截取DG=AF,连接BG,根据SAS可证△ABF≌△DBG,再利用全等三角形的性质证明△GBF是等腰直角三角形,问题即得解决;
(2)在CF上截取CG=EF,连接BG,利用SAS可证△BCG≌△BFE,再利用全等三角形的性质证明△GBF是等腰直角三角形,进一步即可得出结论.
(1)①证明:如图1,∵△ABC绕点B逆时针旋转90°得△DBE,由旋转性质得,△ABC≌△DBE,
∴∠1=∠2,AB=DB,∠ABC=∠DBE=90°,
∵∠1+∠C=90°,
∴∠2+∠C=90°,
∴∠DFC=90°,即DF⊥AC;
②解法一:如图3,连接AD,∵ DF⊥AC,∠DBE=90°,∴ ∠DFA= 90°,
∴A,D,B,F四点均在以AB为直径的圆上,
∵AB=DB ,∠DBE=90°,∴ ∠DAB=45°,
∴∠DFB=∠DAB=45°;

解法二:如图3,在DE上截取DG=AF,连接BG,
在△ABF和△DBG中,
∴△ABF≌△DBG,
∴BF=BG,∠ABF=∠DBG,
∵∠DBA=90°,∴∠GBF=90°,
∴△GBF是等腰直角三角形,
∴∠DFB=45°;
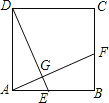
(2)补全图2,如图4;FC-FE=![]() FB.
FB.
证明:如图,在CF上截取CG=EF,连接BG,
在△BCG和△BFE中,
∴△BCG≌△BFE,∴BF=BG,∠CBG=∠EBF,
∵∠ABC=90°,∴∠GBF=90°,
∴△GBF是等腰直角三角形,
∴ ![]() ,
,
∴ FC-FE=FC-CG=![]() .
.


 金博士一点全通系列答案
金博士一点全通系列答案【题目】已知二次函数y =x2 + 4x + 3.
(1)将二次函数的表达式化为y = a (x-h)2 + k 的形式;
(2)在平面直角坐标系xOy中,用描点法画出这个二次函数的图象;
x | … | … | |||||
y | … | … |
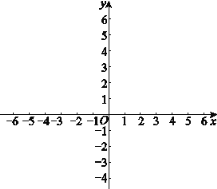
(3)观察图象,直接写出当![]() 时
时![]() 的取值范围;
的取值范围;
(4)根据(2)中的图象,写出一条该二次函数的性质.