题目内容
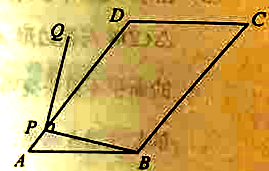
【题目】平面内，如图，在
中，
，
，
．点
为
边上任意一点，连接
，将
绕点
逆时针旋转
得到线段
．
(1)当
时，求
的大小；
(2)当
时，求点
与点
间的距离(结果保留根号)；
(3)若点
恰好落在的边所在的直线上，直接写出
旋转到
所扫过的面积(结果保留
)．
【答案】(1)100°或80°；(2)
；(3)16π或20π或32π.
【解析】
试题分析：(1)根据点Q与点B和PD的位置关系分类讨论；(2)因为△PBQ是等腰直角三角形，所以求BQ的长，只需求PB，过点P作PH⊥AB于点H，确定AH:BH，求得AH和BH，解直角△APH求PH，由勾股定理求PB.(3)根据点Q在AD上，DC上，BC的延长线上，分别画出图形，分三种情况讨论.
试题解析：(1)当点Q与B在PD的异侧时，由∠DPQ=10°，∠BPQ=90°得∠BPD=80°，
∴∠APB=180°-∠BPD=100°.
当点Q与B在PD的同侧时，如图2，∠APB=180°-∠BPQ-∠DPQ=80°.
∴∠APB的度数是80°或100°.
(2)如图2，过点P作PH⊥AB于点H，连接BQ.
∵tan∠ABP:tanA=
，∴AH:HB=3:2.
而AB=10，∴AH=6，HB=4.
在Rt△PHA中，PH=AH·tanA=8.
∴PQ=PB=
.
∴在Rt△PQB中，QB=
PB=
.
(3)①点Q在AD上时，如图3，由tanA=
得，PB=AB·sinA=8，∴扇形面积为16π.
②点A在CD上时，如图4，过点P作PH⊥AB于点H，交CD延长线于点K，由题意∠K=90°，∠KDP=∠A.
设AH=x，则PH=AH·tanA=
.
∵∠BPH=∠KQP=90°-∠KPQ，PB=QP，∴Rt△HPB≌Rt△KQP.∴KP=HB=10-x.
∴AP=
，PD=
，AD=15=
，解得x=6.
∵
，∴扇形的面积为20π.
③点Q在BC延长线上时，如图5，过点B作BM⊥AD于点M，由①得BM=8.
又∠MPB=∠PBQ=45°，∴PB=
，∴扇形面积为32π.
所以扇形的面积为16π或20π或32π.
