题目内容
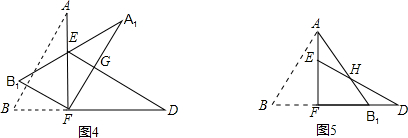
如图，在一张直角三角形纸片，两直角边AC=6，BC=8，将△ABC折叠，使点B与点A重合，折痕为DE，则CD长为
- A.
- B.
- C.
- D.
A
分析：由翻折易得DB=AD，在直角三角形ACD中，利用勾股定理即可求得CD长．
解答：由题意得DB=AD；
设CD=xcm，则
AD=DB=（8-x）cm，
∵∠C=90°，
∴AD2-CD2=AC2（8-x）2-x2=36，
解得x=；
即CD=cm．
故选A．
点评：本题主要考查了折叠问题和勾股定理的综合运用．本题中得到BD=AD是关键．
分析：由翻折易得DB=AD，在直角三角形ACD中，利用勾股定理即可求得CD长．
解答：由题意得DB=AD；
设CD=xcm，则
AD=DB=（8-x）cm，
∵∠C=90°，
∴AD2-CD2=AC2（8-x）2-x2=36，
解得x=
；即CD=
cm．故选A．
点评：本题主要考查了折叠问题和勾股定理的综合运用．本题中得到BD=AD是关键．
练习册系列答案
相关题目
