题目内容
(2012•泉州质检)如图,在直角坐标系中,已知A(0,3)、O(0,0)、C(6,0)、D(3,3),点P从C点出发,沿着折线C-D-A运动到达点A时停止,过C点作直线GC⊥PC,且与过O、P、C三点的⊙M交于点G,连接OP、PG、OD.设点P运动 路线的长度为m.
路线的长度为m.
(1)直接写出∠DCO的度数;
(2)当点P在线段CD上运动时,求△OPG的最小面积;
(3)设圆心M的纵坐标为n,试探索:在点P运动的整个过程中,n的取值范围.
 路线的长度为m.
路线的长度为m.(1)直接写出∠DCO的度数;
(2)当点P在线段CD上运动时,求△OPG的最小面积;
(3)设圆心M的纵坐标为n,试探索:在点P运动的整个过程中,n的取值范围.
分析:(1)过点D作DQ垂直于x轴,如图所示,由D的坐标得到DQ=OQ=3,由C的坐标得到OC=6,由OC-OQ求出CQ=3,可得出DQ=CQ,再由∠DQC为直角,得到三角形DQC为等腰直角三角形,利用等腰直角三角形的性质即可确定出∠DCO为45°;
(2)过P作PB垂直于x轴于点B,由∠DCO为45°,得到三角形PBC为等腰直角三角形,即PB=BC,由P运动的路程为m,得到PC=m,利用勾股定理表示出PB与BC,用OC-BC表示出OB,在直角三角形OPB中,利用勾股定理表示出OP2,根据PC与CG垂直,利用90°的圆周角所对的弦为直径得到PG为圆M的直径,再利用直径所对的圆周角为直角,得到PO与OG垂直,同时利用同弧所对的圆周角相等可得出∠PGO=∠PCO=45°,进而确定出三角形OPG为等腰直角三角形,即PO=OG,三角形POG的面积等于两直角边乘以的一半,即为
OP2,将表示出的OP2代入,可得其面积为关于m的二次函数,其图象开口向上,有最小值,其对称轴为直线x=3
,且当0<m≤3
时,S△OPG随m的增大而减小,利用二次函数的性质即可求出此时S△OPG的最小值;
(3)由OQ=CQ=DQ,DQ垂直于x轴,得到三角形DOC为等腰直角三角形,即OD=CD,过M作MN垂直于x轴,利用垂径定理得到N为OC的中点,可得出DN为OC的垂直平分线,连接OM,分两种情况考虑:(i)当P在DC边上时,如左图可知:∠OPC为钝角或直角,点M在x轴下方(或x轴上),由三角形OPM为等腰直角三角形,可得出OP=
OM,表示出OM,又ON为3,利用勾股定理表示出MN2,将(2)得出的OP2代入,得到关于m的二次函数,利用m的范围即可求出n的范围;(ii)当点P在AD边上时,如右图所示,由圆的半径相等得到OM=PM,在直角三角形PDM中,由PD=m-3
,DM=3-n,利用勾股定理表示出PM2,在直角三角形OMN中,由ON=3,MN=n,利用勾股定理表示出OM2,两者相等列出关于m与n的关系式,用m表示出n,根据m的范围即可求出n的范围,综上,得到满足题意的n的范围.
(2)过P作PB垂直于x轴于点B,由∠DCO为45°,得到三角形PBC为等腰直角三角形,即PB=BC,由P运动的路程为m,得到PC=m,利用勾股定理表示出PB与BC,用OC-BC表示出OB,在直角三角形OPB中,利用勾股定理表示出OP2,根据PC与CG垂直,利用90°的圆周角所对的弦为直径得到PG为圆M的直径,再利用直径所对的圆周角为直角,得到PO与OG垂直,同时利用同弧所对的圆周角相等可得出∠PGO=∠PCO=45°,进而确定出三角形OPG为等腰直角三角形,即PO=OG,三角形POG的面积等于两直角边乘以的一半,即为
| 1 |
| 2 |
| 2 |
| 2 |
(3)由OQ=CQ=DQ,DQ垂直于x轴,得到三角形DOC为等腰直角三角形,即OD=CD,过M作MN垂直于x轴,利用垂径定理得到N为OC的中点,可得出DN为OC的垂直平分线,连接OM,分两种情况考虑:(i)当P在DC边上时,如左图可知:∠OPC为钝角或直角,点M在x轴下方(或x轴上),由三角形OPM为等腰直角三角形,可得出OP=
| 2 |
| 2 |
解答:解:(1)过D作DQ⊥x轴于点Q,如图所示:
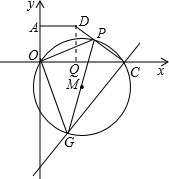 由D(3,3),得到DQ=OQ=3,由C(6,0),得到OC=6,
由D(3,3),得到DQ=OQ=3,由C(6,0),得到OC=6,
∴QC=OC-OQ=6-3=3,即DQ=CQ,又∠DQC=90°,
∴△DQC为等腰直角三角形,
∴∠DCO=45°;
(2)过点P作PB⊥x轴于点B,可得△PBC为等腰直角三角形,
∵PC=m,∴PB=BC=
m,
在Rt△POB中,OB=OC-BC=6-
m,PB=
m,
根据勾股定理得:OP2=(
m)2+(6-
m)2,
∵GC⊥PC,
∴PG为⊙M的直径,
∴∠POG=90°,又∠OGP=∠PCO=45°,
∴△OPG为等腰直角三角形,
∴PO=OG,
∴S△OPG=
OP•OG=
OP2=
[(
m)2+(6-
m)2]=
(m-3
)2+9,
∵S△OPG是关于m的二次函数,其图象开口向上,有最小值,其对称轴为直线x=3
,
∴当0<m≤3
时,S△OPG随m的增大而减小,
则m=3
时,S△OPG取得最小值为9;
(3)由题意得:∠ODC=90°,△OPC的外心M必在OC的垂直平分线上,
作MN⊥x轴于点N,则ON=
OC=3,可得直线MN经过点D,连接OM.
分两种情况考虑:
(i)当点P在CD上,即0<m≤3
时,如左图可知:∠OPC为钝角或直角,
∴点M在x轴下方(或x轴上),
又由(2)得:OM=
OP,ON=3,又OP2=(
m)2+(6-
m)2,
在Rt△MON中,MN2=OM2-ON2=(
OP)2-32=
(m-3
)2+9-9=
(m-3
)2,
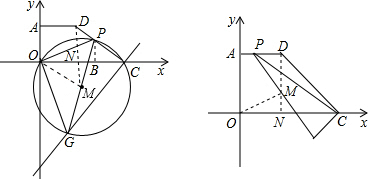 ∵0<m≤3
∵0<m≤3
,
∴n的取值范围是:-3<n≤0;
(ii)当点P在AD上,即3
<m≤3
+3时,如右图,依题意得:MO=PM,
由勾股定理得:ON2+MN2=DM2+PD2,
又ON=3,MN=n,DM=3-n,PD=m-3
,
∴32+n2=(3-n)2+(m-3
)2,
整理得:n=
(m-3
)2,
∵3
<m≤3
+3,
∴0<n≤
,
综上,得到n的取值范围是:-3<n≤
.
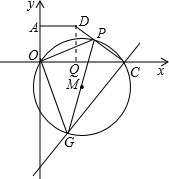 由D(3,3),得到DQ=OQ=3,由C(6,0),得到OC=6,
由D(3,3),得到DQ=OQ=3,由C(6,0),得到OC=6,∴QC=OC-OQ=6-3=3,即DQ=CQ,又∠DQC=90°,
∴△DQC为等腰直角三角形,
∴∠DCO=45°;
(2)过点P作PB⊥x轴于点B,可得△PBC为等腰直角三角形,
∵PC=m,∴PB=BC=
| ||
| 2 |
在Rt△POB中,OB=OC-BC=6-
| ||
| 2 |
| ||
| 2 |
根据勾股定理得:OP2=(
| ||
| 2 |
| ||
| 2 |
∵GC⊥PC,
∴PG为⊙M的直径,
∴∠POG=90°,又∠OGP=∠PCO=45°,
∴△OPG为等腰直角三角形,
∴PO=OG,
∴S△OPG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
∵S△OPG是关于m的二次函数,其图象开口向上,有最小值,其对称轴为直线x=3
| 2 |
∴当0<m≤3
| 2 |
则m=3
| 2 |
(3)由题意得:∠ODC=90°,△OPC的外心M必在OC的垂直平分线上,
作MN⊥x轴于点N,则ON=
| 1 |
| 2 |
分两种情况考虑:
(i)当点P在CD上,即0<m≤3
| 2 |
∴点M在x轴下方(或x轴上),
又由(2)得:OM=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
在Rt△MON中,MN2=OM2-ON2=(
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
 ∵0<m≤3
∵0<m≤3| 2 |
∴n的取值范围是:-3<n≤0;
(ii)当点P在AD上,即3
| 2 |
| 2 |
由勾股定理得:ON2+MN2=DM2+PD2,
又ON=3,MN=n,DM=3-n,PD=m-3
| 2 |
∴32+n2=(3-n)2+(m-3
| 2 |
整理得:n=
| 1 |
| 6 |
| 2 |
∵3
| 2 |
| 2 |
∴0<n≤
| 3 |
| 2 |
综上,得到n的取值范围是:-3<n≤
| 3 |
| 2 |
点评:此题属于圆的综合题,涉及的知识有:坐标与图形性质,等腰直角三角形的判定与性质,勾股定理,圆周角定理,利用了转化及分类讨论的思想,探讨此类问题时要注意各问之间的联系,下一问要运用上一问的结论.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 (2012•泉州质检)如图,点A在半径为3的⊙O上,过点A的切线与OB的延长线交于点C,∠C=30°,则图中AB的长为
(2012•泉州质检)如图,点A在半径为3的⊙O上,过点A的切线与OB的延长线交于点C,∠C=30°,则图中AB的长为