��Ŀ����
����Ŀ��ʵ���������������ѧϰ�ı��ε����֪ʶʱ����ʶ��ƽ���ı��Ρ����Ρ����Ρ������ε�һЩ������ı��Σ����������ó߹���ͼ�ķ������������֮�����ϵ����ͼ����ABCD�У�AB=4��BC=6����ABC=60�㣬������������� 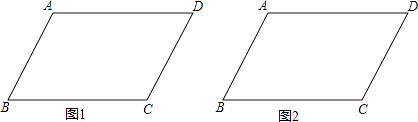
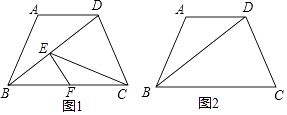
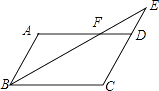
��1����ͼ1����һ�����Σ�ʹ�õ�A��BΪ�������ε�2�����㣬����2��������ABCD�ı��ϣ���ͼ2����һ�����Σ�ʹ��B��DΪ�������ε�2�����㣬����2��������ABCD�ı��ϣ����߹���ͼ��������ͼ�ۼ�����д������
��2������ͼ���·����ߴ�ֱ��д���㰴��1����Ҫ�����������ε������
���𰸡�
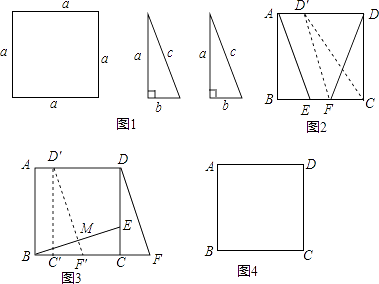
��1���⣺��ͼ��ʾ��
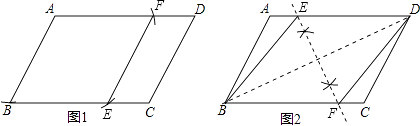
��2���⣺��ͼ1����ABCD�ĸ�AH��
��ֱ�ǡ�ABH�У���AB=4����ABC=60�㣬
��AH=ABsin60��=4�� ![]() =2
=2 ![]() ��BH=ABcos60��=4��
��BH=ABcos60��=4�� ![]() =2��
=2��
��S����ABEF=BEAH=4��2 ![]() =8
=8 ![]() ��
��
��ͼ2����BD��EF���ڵ�O����DM��BC��M����CM=BH=2��DM=AH=2 ![]() ��
��
��ֱ�ǡ�BDM�У��ߡ�M=90�㣬
��BD= ![]() =
= ![]() =2
=2 ![]() ��
��
��BF=x��CF=y����DF=x��
������� ![]() ��
��
��� 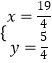 ��
��
��OF= ![]() =
= ![]() =
= ![]() ��
��
��S����ABEF= ![]() BDEF=
BDEF= ![]() ��2
��2 ![]() ��
�� ![]() =
= ![]() ��
��
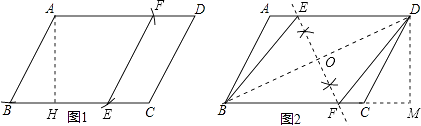
����������1����ͼ1����AD��BC�Ϸֱ��ȡAF=BE=4������EF�����ı���ABEF�����Σ���ͼ2������BD����BD�Ĵ�ֱƽ���ߣ���AD��E��BC��F�����ı���BEDF�����Σ���2����ͼ1����ABCD�ĸ�AH���������ε����=�ס�����ʽ���㼴�ɣ���ͼ2����BD��EF���ڵ�O����DM��BC��M����CM=BH=2��DM=AH=2 ![]() ���ֱ����BD��EF���������ε����=���Խ��߳˻���һ����ʽ���㼴�ɣ�
���ֱ����BD��EF���������ε����=���Խ��߳˻���һ����ʽ���㼴�ɣ�
�����㾫����������Ĺؼ���������ƽ���ı��ε����ʵ����֪ʶ������ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣��Լ������ε����ʵ����⣬�˽����ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룮