题目内容
已知m2+n2-4m-2n+5=0,求m+n的值.
考点:因式分解-运用公式法,非负数的性质:偶次方
专题:
分析:利用完全平方公式配方进而得出m,n的值.
解答:解:∵m2+n2-4m-2n+5=0,
∴(m-2)2+(n-1)2=0,
解得:m=2,n=1,
∴m+n=3.
∴(m-2)2+(n-1)2=0,
解得:m=2,n=1,
∴m+n=3.
点评:本题主要考查配方法的应用、非负数性质的应用,难度适中,是常见的题型.解答这类问题的关键是要熟练掌握配方法的要点,掌握“若干个非负数的和等于0,则每个非负数均等于0“这一重要性质.

练习册系列答案
相关题目
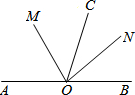 已知:A、O、B在同一直线上,OC是任意一条射线,OM、ON分别为∠AOC、∠BOC的平分线,求∠MON的度数并说明理由.
已知:A、O、B在同一直线上,OC是任意一条射线,OM、ON分别为∠AOC、∠BOC的平分线,求∠MON的度数并说明理由.