题目内容
已知:直角梯形OABC中,CB∥OA,对角线OB和AC交于点D,OC=2,CB=2,OA=4,点P为对角线CA上的一点,过点P作QH⊥OA于H,交CB的延长线于点Q,连接BP,如果△BPQ∽△PHA,则点P的坐标为 .
【答案】分析:先根据点A、点C的坐标利用待定系数法求出直线AC的解析式,当HQ在点B的左侧时和QH在点B的右侧时利用相似三角形的性质就可以求出点P的坐标.
解答:解:∵OC=2,OA=4,
∴C(0,2),A(4,0).
设直线AC的解析式为y=kx+b,由题意,得
 ,
,
解得 ,
,
故直线AC的解析式为:y=- x+2.
x+2.
如图2,在点B的右侧,当△BQP∽△AHP时,
则 ,
,
则BQ.PH=AH.PQ.
∵点P在直线AC上,设点P的坐标为(x,- x+2)(0<x<4),
x+2)(0<x<4),
∴CQ=x,OH=x,PH=- x+2,
x+2,
∵CB=2,OA=4,OH=2,
∴BQ=x-2,AH=4-x,PQ= x.
x.
∴(x-2)(- x+2)=(4-x)(
x+2)=(4-x)( x),
x),
解得x=4(舍去).
当△BQP∽△PHA时,
则 ,即BQ.AH=PH.PQ,
,即BQ.AH=PH.PQ,
(x-2)(4-x)=(- x+2)(
x+2)( x),
x),
解得x1= ,x2=4(舍去)
,x2=4(舍去)
则y= ,
,
则P( ,
, ).
).
∴P( ,
, ).
).
故答案为:P( ,
, ).
).

点评:本题是一道相似三角形的综合试题,考查了相似三角形的性质的运用,待定系数法求直线的解析式的运用及分类讨论思想的运用.本题难度较大,涉及的情况较多,解答时不要漏解.
解答:解:∵OC=2,OA=4,
∴C(0,2),A(4,0).
设直线AC的解析式为y=kx+b,由题意,得
 ,
,解得
 ,
,故直线AC的解析式为:y=-
 x+2.
x+2.如图2,在点B的右侧,当△BQP∽△AHP时,
则
 ,
,则BQ.PH=AH.PQ.
∵点P在直线AC上,设点P的坐标为(x,-
 x+2)(0<x<4),
x+2)(0<x<4),∴CQ=x,OH=x,PH=-
 x+2,
x+2,∵CB=2,OA=4,OH=2,
∴BQ=x-2,AH=4-x,PQ=
 x.
x.∴(x-2)(-
 x+2)=(4-x)(
x+2)=(4-x)( x),
x),解得x=4(舍去).
当△BQP∽△PHA时,
则
 ,即BQ.AH=PH.PQ,
,即BQ.AH=PH.PQ,(x-2)(4-x)=(-
 x+2)(
x+2)( x),
x),解得x1=
 ,x2=4(舍去)
,x2=4(舍去)则y=
 ,
,则P(
 ,
, ).
).∴P(
 ,
, ).
).故答案为:P(
 ,
, ).
).
点评:本题是一道相似三角形的综合试题,考查了相似三角形的性质的运用,待定系数法求直线的解析式的运用及分类讨论思想的运用.本题难度较大,涉及的情况较多,解答时不要漏解.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
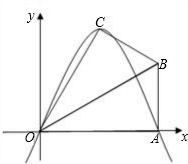 线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处. 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S. 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
