题目内容
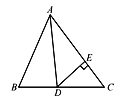
【题目】如图,在正方形ABCD中,E、F分别是边BC、CD上的点,![]() =
=![]() ,CF=DF,连接AE、AF、EF,并延长FE交AB的延长线于点G.
,CF=DF,连接AE、AF、EF,并延长FE交AB的延长线于点G.
(1)若正方形的边长为4,则EG等于 ;
(2)求证:△ECF∽△FDA;
(3)比较∠EAB与∠EAF的大小.

【答案】(1)3![]() ;(2)证明参见解析;(3)∠EAF<∠EAB.
;(2)证明参见解析;(3)∠EAF<∠EAB.
【解析】
试题分析:(1)先根据正方形边长得CF=2,由平行相似得:△FCE∽△GBE,则![]() ,代入求得BG=6,根据勾股定理得:EG=3
,代入求得BG=6,根据勾股定理得:EG=3![]() ;(2)根据已知边的长度分别求
;(2)根据已知边的长度分别求![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,则
,则![]() =
=![]() ,再由正方形性质得:∠C=∠D=90°,则△ECF∽△FDA;(3)先根据(2)中的△ECF∽△FDA,得∠CFE=∠DAF,
,再由正方形性质得:∠C=∠D=90°,则△ECF∽△FDA;(3)先根据(2)中的△ECF∽△FDA,得∠CFE=∠DAF,![]() =
=![]() =
=![]() ,证明∠EFA=90°,分别计算∠EAB与∠EAF的正切值,根据两锐角正切大的角大,得出结论.
,证明∠EFA=90°,分别计算∠EAB与∠EAF的正切值,根据两锐角正切大的角大,得出结论.
试题解析:(1)∵四边形ABCD是正方形,∴AB=CD=BC=4,∠ABC=90°,DC∥AB,∵CF=DF,∴CF=![]() CD=2,
CD=2,
∵DC∥AG,∴△FCE∽△GBE,∴![]() ,∵
,∵![]() =
=![]() ,∴
,∴![]() =
=![]() ,BE=
,BE=![]() BC=
BC=![]() ×4=3,∴
×4=3,∴![]() =
=![]() ,∴BG=6,在Rt△BEG中,EG=
,∴BG=6,在Rt△BEG中,EG=![]() =
=![]() =3
=3![]() ;故答案为:3
;故答案为:3![]() ;(2)∵四边形ABCD是正方形,∴BC=AD=DC=4,∠C=∠D=90°,∵DF=FC=2,CE=1,∴
;(2)∵四边形ABCD是正方形,∴BC=AD=DC=4,∠C=∠D=90°,∵DF=FC=2,CE=1,∴![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴△ECF∽△FDA;(3)∵△ECF∽△FDA,∴∠CFE=∠DAF,
,∴△ECF∽△FDA;(3)∵△ECF∽△FDA,∴∠CFE=∠DAF,![]() =
=![]() =
=![]() ,∵∠DFA+∠DAF=90°,∴∠CFE+∠DFA=90°,∴∠EFA=90°,∴tan∠EAF=
,∵∠DFA+∠DAF=90°,∴∠CFE+∠DFA=90°,∴∠EFA=90°,∴tan∠EAF=![]() =
=![]() ,∵
,∵![]() =
=![]() ,∴tan∠EAB=
,∴tan∠EAB=![]() =
=![]() ,∵
,∵![]() <
<![]() ,∴∠EAF<∠EAB.
,∴∠EAF<∠EAB.

练习册系列答案
相关题目