题目内容
已知关于 的方程:
的方程: ①和
①和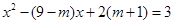 ②,其中
②,其中 .
.
(1)求证:方程①总有两个不相等的实数根;
(2)设二次函数 的图象与
的图象与 轴交于
轴交于 、
、 两点(点
两点(点 在点
在点 的左侧),将
的左侧),将 、
、 两点按照相同的方式平移后,点
两点按照相同的方式平移后,点 落在点
落在点 处,点
处,点 落在点
落在点 处,若点
处,若点 的横坐标恰好是方程②的一个根,求
的横坐标恰好是方程②的一个根,求 的值;
的值;
(3)设二次函数 ,在(2)的条件下,函数
,在(2)的条件下,函数 ,
, 的图象位于直线
的图象位于直线 左侧的部分与直线
左侧的部分与直线 (
( )交于两点,当向上平移直线
)交于两点,当向上平移直线 时,交点位置随之变化,若交点间的距离始终不变,则
时,交点位置随之变化,若交点间的距离始终不变,则 的值是________________.
的值是________________.
(1)证明见解析;(2)3;(3) .
.
解析试题分析:(1)证明方程根的判别式大于0即可.
(2)根据平移的性质,得到点 平移后的坐标
平移后的坐标 ,由点
,由点 的横坐标恰好是方程②的一个根,代入求解即可.
的横坐标恰好是方程②的一个根,代入求解即可.
(3)求出过两抛物线的顶点的直线的 即为所求.
即为所求.
试题解析:(1) ,
,
由 知必有
知必有 ,故
,故 .
.
∴方程①总有两个不相等的实数根.
(2)令 ,依题意可解得
,依题意可解得 ,
, .
.
∵平移后,点 落在点
落在点 处,
处,
∴平移方式是将点 向右平移2个单位,再向上平移3个单位得到.
向右平移2个单位,再向上平移3个单位得到.
∴点 按相同的方式平移后,点
按相同的方式平移后,点 为
为 .
.
则依题意有 .
.
解得 ,
, (舍负).
(舍负).
∴ 的值为3.
的值为3.
(3)在(2)的条件下, ,
,
两抛物线的顶点坐标分别为 ,则过这两点的直线解析式为
,则过这两点的直线解析式为 .
.
∴ .
.
考点:1.一元二次方程根的判别式;2.二次函数的性质;3.待定系数法的应用;4.曲线上点的坐标与方程的关系;5.平移的性质.

练习册系列答案
相关题目
 (其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE. 为定值;
为定值;

 与
与 交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①
交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:① ;②
;② 时,
时, ;③平行于x轴的直线
;③平行于x轴的直线 与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )
与两条抛物线有四个交点;④2AB=3AC.其中错误结论的个数是( )
 的图象经过(
的图象经过( ,0)和(
,0)和( ,0)两点.
,0)两点. <x<1时,y的取值范围.
<x<1时,y的取值范围.
 (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
 与
与 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
 =7.14,
=7.14, =7.21,
=7.21, =7.28,
=7.28,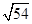 =7.35)
=7.35)