Question

【题目】如图在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，D为斜边AB上一点，以CD、CB为边作平行四边形CDEB ， 当AD＝ ， 平行四边形CDEB为菱形．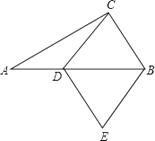

Answer 1

【答案】?
【解析】如图，连接CE交AB于点O ． ∵Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，∴AB＝ （勾股定理）．若平行四边形CDEB为菱形时，CE⊥BD ， 且OD＝OB ， CD＝CB ． ∵ ABOC＝ ACBC ， ∴OC＝ ．∴在Rt△BOC中，根据勾股定理得，OB＝ ，∴AD＝AB－2OB＝ ．

【考点精析】通过灵活运用勾股定理的概念和菱形的判定方法，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形即可以解答此题．