题目内容
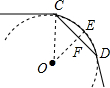
如图所示,某窗户有矩形和弓形组成,已知弓形的跨度AB=3cm,弓形的高EF=1cm,现计划安装玻璃,请帮工程师求出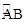 所在圆O的半径r.
所在圆O的半径r.
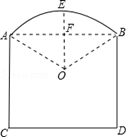
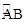 所在圆O的半径r.
所在圆O的半径r.
解:∵弓形的跨度AB=3cm,EF为弓形的高,∴OE⊥AB。∴AF= AB=
AB= cm。
cm。
∵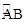 所在圆O的半径为r,弓形的高EF=1cm,∴AO=r,OF=r﹣1。
所在圆O的半径为r,弓形的高EF=1cm,∴AO=r,OF=r﹣1。
在Rt△AOF中,AO2=AF2+OF2,即r2=( )2+(r﹣1)2,解得r=
)2+(r﹣1)2,解得r= cm。
cm。
答: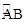 所在圆O的半径为
所在圆O的半径为 cm。
cm。
 AB=
AB= cm。
cm。∵
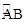 所在圆O的半径为r,弓形的高EF=1cm,∴AO=r,OF=r﹣1。
所在圆O的半径为r,弓形的高EF=1cm,∴AO=r,OF=r﹣1。在Rt△AOF中,AO2=AF2+OF2,即r2=(
 )2+(r﹣1)2,解得r=
)2+(r﹣1)2,解得r= cm。
cm。答:
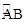 所在圆O的半径为
所在圆O的半径为 cm。
cm。根据垂径定理可得AF= AB,再表示出AO、OF,然后利用勾股定理列式进行计算即可得解。
AB,再表示出AO、OF,然后利用勾股定理列式进行计算即可得解。
 AB,再表示出AO、OF,然后利用勾股定理列式进行计算即可得解。
AB,再表示出AO、OF,然后利用勾股定理列式进行计算即可得解。
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
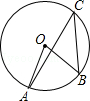
 ,则图中阴影部分的面积为
,则图中阴影部分的面积为






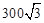 米,则这段弯路的长度为
米,则这段弯路的长度为