题目内容
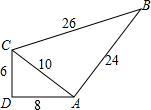一个零件的形状如图所示，按规定这个零件中∠BAC和∠ADC都应为直角，工人师傅量的零件各边尺寸：AD=8，AC=10，CD=6，AB=24，BC=26，请你判断这个零件是否符合要求，并说明理由．考点：勾股定理的逆定理
专题：应用题
分析：根据勾股定理的逆定理，判断出△ACD、△ABC的形状，从而判断这个零件是否符合要求．
解答：解：∵AD=8，AC=10，CD=6，AB=24，BC=26，
∴AD2+CD2=AC2，AB2+AC2=BC2，
∴△ACD、△ABC是直角三角形，
∴∠ADC=90°，∠BAC=90°，
故这个零件符合要求．
∴AD2+CD2=AC2，AB2+AC2=BC2，
∴△ACD、△ABC是直角三角形，
∴∠ADC=90°，∠BAC=90°，
故这个零件符合要求．
点评：本题考查了勾股定理的逆定理，关键是根据勾股定理的逆定理判断△ACD、△ABC的形状．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
课课优能力培优100分系列答案
优百分课时互动系列答案
相关题目
已知，如图，AB∥CD，∠BEF与∠EFD的角平分线相交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，证明：PF∥GH．
如图，AO⊥BC，DO⊥OE．求证：∠AOD=∠COE，∠BOD=∠AOE．