题目内容
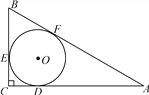
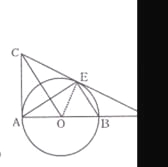
【题目】如图，以线段AB为直径作⊙O，CD与⊙O相切于点E，交AB的延长线于点D， 连接BE，过点O作OC∥BE交切线DE于点C，连接AC ．
（1）求证：AC是⊙O的切线 ；
（2）若BD=OB=4，求弦AE的长．
【答案】（1）见解析；（2）
．
【解析】
试题（1）连结OE，根据条件证明△AOC≌△EOC，进而得出∠CAO=∠CEO =90°即可；（2）利用直角三角形的性质和特殊角的三角函数值，可求出线段AE的长．
试题解析：（1）证明：连结OE，
因为CD与⊙O相切于点E，所以OE
CD，所以∠CEO =90°，
因为OC∥BE，所以∠AOC=∠OBE，∠COE=∠OEB，
因为OB=OE，所以∠OBE=∠OEB，所以∠AOC=∠COE，
因为OA=OE，OC=OC， 所以△AOC≌△EOC，
所以∠CAO=∠CEO =90°， 所以AC是⊙O的切线 ；
（2）解：在Rt△DEO中，因为BD=OB， 所以BE=
OD=OB=4，
又因为OB=OE， 所以△AOC是等边三角形，所以∠ABE=60°，
因为AB为直径，所以∠AEB=90°，
在Rt△ABE中，AE=tan60°
BE=．
练习册系列答案
相关题目
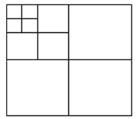
【题目】如图，将一张正方形纸片，剪成四个大小形状一样的小正方形，然后将其中的一个小正方形再按同样的方法剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去；
（1）填表
剪的次数 | 1 | 2 | 3 | 4 | 5 |
正方形个数 | 4 | 7 | 10 |
|
|
（2）如果剪n次，共剪出多少个小正方形？
（3）能否经过若干次分割后共得到2019片纸片？若能，请直接写出相应的次数，若不能，请说明理由．
