Question

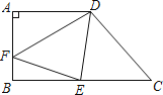
【题目】已知：如图，四边形ABCD中，AD∥BC，∠B=90°，AD=AB=4，BC=7，点E在BC上，将△CDE沿DE折叠，点C恰好落在AB边上的点F处．

（1）求线段DC的长度；

（2）求△FED的面积．

Answer 1

【答案】（1）5；（2）

【解析】

（1）通过证明四边形ABMD是正方形，可得DM=BM=AB=4，CM=3，由勾股定理可求CD的长．

（2）由折叠的性质可得EF=CE，DC=DF=5，由“HL“可证Rt△ADF≌Rt△MDC，可得AF=CM=3，由勾股定理可求EC的长，即可求解．

解：（1）过点D作DM⊥BC于M．

∵AD∥BC，∠B=90°，

∴∠A=90°，且∠B=90°，DM⊥BC，

∴四边形ABMD是矩形，且AD=AB，

∴四边形ABMD是正方形．

∴DM=BM=AB=4，CM=3，

在Rt△DMC中，CD===5，

（2）∵将△CDE沿DE折叠，

∴EF=CE，DC=DF=5，且AD=DM，

∴Rt△ADF≌Rt△MDC（HL），

∴AF=CM=3，

∴BF=1，

∵EF2=BF2+BE2，

∴CE2=1+（7-CE）2，

∴CE=

∴S△FED=×CE×DM=×=