题目内容
 如图所示,已知⊙O1与⊙O2切于点P,外公切线AB与连心线O1O2相交于点C,A、B是切点,D是AP延长线上的点,满足
如图所示,已知⊙O1与⊙O2切于点P,外公切线AB与连心线O1O2相交于点C,A、B是切点,D是AP延长线上的点,满足| AP |
| AB |
| AC |
| AD |
| 4 |
| 5 |
求:(1)cosD;(2)S⊙O1:S⊙O2的值.
分析:(1)过P作两圆的内公切线交AB于Q,连接PB.得到QA=QP=QB,根据∠APB=90°
=
,得到△CAD∽△PAB,推出∠ACD=∠APB=90°设AC=4t,AD=5t,则CD=3t,即可求出答案;
(2)在Rt△APB中,设AP=8a,AB=10a,则PB=6a.作O1E⊥AP于E,O1F⊥BP于F,得到EP=
AP=4a,FP=3a,根据∠FO2P=∠APB=∠D,推出Rt△PFQ2∽Rt△ACD,得到
=
=
,根据O1E∥PF,得到△EO1P∽△FPO2,求
,根据相似三角形的性质即可求出答案.
| AP |
| AB |
| AC |
| AD |
(2)在Rt△APB中,设AP=8a,AB=10a,则PB=6a.作O1E⊥AP于E,O1F⊥BP于F,得到EP=
| 1 |
| 2 |
| FO2 |
| PF |
| CD |
| CA |
| 3 |
| 4 |
| O1P |
| O2P |
解答: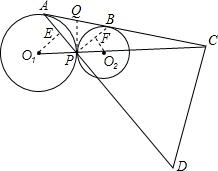 解:(1)过P作两圆的内公切线交AB于Q,连接PB.
解:(1)过P作两圆的内公切线交AB于Q,连接PB.
∵AB是两圆的外公切线,
∴QA=QP=QB,
∴∠APB=90°
∵
=
,即
=
,∠CAD=∠PAB,
∴△CAD∽△PAB,
∴∠ACD=∠APB=90°,
在Rt△ACD中,令AC=4t,AD=5t,则CD=3t,
∴cosD=
=
,
答:cosD=
.
(2)解:在Rt△APB中,设AP=8a,AB=10a,则PB=6a.
作O1E⊥AP于E,O2F⊥BP于F,
则EP=
AP=4a,FP=3a,
在Rt△PO2F中,∠FO2P=∠D,∠PFO2=∠ACD=90°,
∴△PFO2∽△ACD,
∴
=
=
,
∵PF=3a,
∴FO2=
a,
又O1E∥PF,∠EO1P=∠FPO2,
∴△EO1P∽△FPO2,
∴
=
=
=
,
∴
=(
)2=
,
答:S⊙O1:S⊙O2的值是
.
 解:(1)过P作两圆的内公切线交AB于Q,连接PB.
解:(1)过P作两圆的内公切线交AB于Q,连接PB.∵AB是两圆的外公切线,
∴QA=QP=QB,
∴∠APB=90°
∵
| AP |
| AB |
| AC |
| AD |
| AD |
| AB |
| AC |
| AP |
∴△CAD∽△PAB,
∴∠ACD=∠APB=90°,
在Rt△ACD中,令AC=4t,AD=5t,则CD=3t,
∴cosD=
| CD |
| AD |
| 3 |
| 5 |
答:cosD=
| 3 |
| 5 |
(2)解:在Rt△APB中,设AP=8a,AB=10a,则PB=6a.
作O1E⊥AP于E,O2F⊥BP于F,
则EP=
| 1 |
| 2 |
在Rt△PO2F中,∠FO2P=∠D,∠PFO2=∠ACD=90°,
∴△PFO2∽△ACD,
∴
| FO2 |
| PF |
| CD |
| CA |
| 3 |
| 4 |
∵PF=3a,
∴FO2=
| 9 |
| 4 |
又O1E∥PF,∠EO1P=∠FPO2,

∴△EO1P∽△FPO2,
∴
| O1P |
| O2P |
| PE |
| O2F |
| 4a | ||
|
| 16 |
| 9 |
∴
| S⊙o1 |
| S⊙o2 |
| o1P |
| o2P |
| 256 |
| 81 |
答:S⊙O1:S⊙O2的值是
| 256 |
| 81 |
点评:本题主要考查对切线长定理,平行线分线段成比例定理,相似三角形的性质和判定,相切两圆的性质,锐角三角函数的定义等知识点的理解和掌握,熟练地运用这些性质进行推理是解此题的关键,题型较好,综合性强,难度适中.

练习册系列答案
相关题目
 如图所示,已知⊙O1和⊙O2的半径分别为5和
如图所示,已知⊙O1和⊙O2的半径分别为5和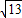 ,它们的公共弦AB=6,求O1O2的长.
,它们的公共弦AB=6,求O1O2的长.
 .
. 的值.
的值.
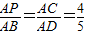 .
. 的值.
的值.