题目内容
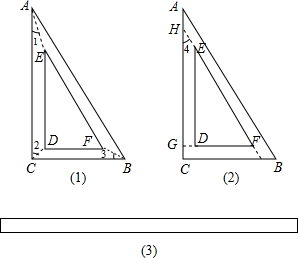
 劳技课上,同学们领到了一根长方形木条(图3),班长倡议:我们用锯子分割一下,然后用强力胶粘起来,为数学老师做一把有一个角30°的直角三角板.于是同学们分成甲乙两个组,进行探究:
劳技课上,同学们领到了一根长方形木条(图3),班长倡议:我们用锯子分割一下,然后用强力胶粘起来,为数学老师做一把有一个角30°的直角三角板.于是同学们分成甲乙两个组,进行探究:①甲小组对图形进行了分析探究,得到方案一:
如图(1),连结AE、CD、BF,则∠1=
15°
15°
;∠2=45°
45°
;乙小组对图形进行了分析探究,得到方案二:
如图(2),延长FE、FD,以及连结BF,则∠4=
30°
30°
.②两个小组比较后,认为图(1)虽然美观,但是图(2)更方便计算,决定以图(2)为操作方案,若制成后的三角板中,AB与EF的距离是5,DF=30,则图(3)中矩形宽=
5
5
;长至少等于105+40
| 3 |
105+40
;| 3 |
③现在甲乙两个小组手中的矩形木条尺寸6×120(图3),在裁剪粘贴中不计损耗,则制成的最大三角板中,DF的长是多少?(在裁剪中,不改变图(3)中木条的宽度)
分析:①根据剪拼的性质,∠1、∠2分别为∠A、∠C的角平分线,然后求解即可;根据两直线平行,同位角相等可得∠4=∠A;
②根据AB、EF间的距离等于木条的宽度解答;根据剪拼的特点,木条的长度=GF+EF+ED+AH+HE+BK,然后根据DF=30,矩形木条的宽度是5进行计算即可得解;
③设DF=x,然后根据木条的长度=GF+EF+ED+AH+HE+BK列出方程求解即可.
②根据AB、EF间的距离等于木条的宽度解答;根据剪拼的特点,木条的长度=GF+EF+ED+AH+HE+BK,然后根据DF=30,矩形木条的宽度是5进行计算即可得解;
③设DF=x,然后根据木条的长度=GF+EF+ED+AH+HE+BK列出方程求解即可.
解答:解:①∠1=
×30°=15°,
∠2=
×90°=45°,
∠4=∠A=30°;
②∵AB与EF的距离是5,
∴矩形宽=5,
矩形木条的长度=GF+EF+ED+AH+HE+BF,
=30+5+2×30+30
+5
+5×2+5
,
=105+40
;
故答案为:①15°,45°,30°;②5,105+40
.
③设DF=x,根据题意得,
(x+6)+2x+
x+6
+12+6
=120,
解得:x=
=57-23
,
答:DF的长为57-23
.
| 1 |
| 2 |
∠2=
| 1 |
| 2 |
∠4=∠A=30°;

②∵AB与EF的距离是5,
∴矩形宽=5,
矩形木条的长度=GF+EF+ED+AH+HE+BF,
=30+5+2×30+30
| 3 |
| 3 |
| 3 |
=105+40
| 3 |
故答案为:①15°,45°,30°;②5,105+40
| 3 |
③设DF=x,根据题意得,
(x+6)+2x+
| 3 |
| 3 |
| 3 |
解得:x=
102-12
| ||
3+
|
| 3 |
答:DF的长为57-23
| 3 |
点评:本题考查了图形的剪拼,根据图形的拼接处确定出矩形木条的长度的表示是解题的关键,也是本题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 劳技课上,同学们领到了一根长方形木条(图3),班长倡议:我们用锯子分割一下,然后用强力胶粘起来,为数学老师做一把有一个角30°的直角三角板.于是同学们分成甲乙两个组,进行探究:
劳技课上,同学们领到了一根长方形木条(图3),班长倡议:我们用锯子分割一下,然后用强力胶粘起来,为数学老师做一把有一个角30°的直角三角板.于是同学们分成甲乙两个组,进行探究: