题目内容
(2010•硚口区模拟)在△ABC中,BD是△ABC的中线,点P为BD上一点,且BP=2PD,过点P作MN∥BC交AB于点M,交AC于点N.
(1)如图一,若BA=BC,写出图中所有与PM相等的线段,并分别给出证明;
(2)如图二,过BA≠BC,在(1)中与PM相等的线段中找出一条仍然与PM相等的线段,并给出证明.
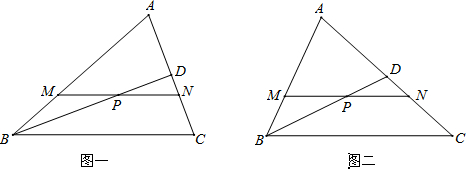
(1)如图一,若BA=BC,写出图中所有与PM相等的线段,并分别给出证明;
(2)如图二,过BA≠BC,在(1)中与PM相等的线段中找出一条仍然与PM相等的线段,并给出证明.

分析:(1)首先过点M作ME∥AC,由在△ABC中,BD是△ABC的中线,BA=BC,根据三线合一的性质,可得BD是高,是角平分线,又由MN∥BC,易证得△PMB是等腰三角形,即可得PM=BM,然后证得PE=PD,即可证得△PME≌△PND,继而证得PM=PN;
(2)首先过点M作ME∥AC,根据平行线分线段成比例定理,易证得ME=DN=
CD,则可证得△PME≌△PND,继而证得PM=PN.
(2)首先过点M作ME∥AC,根据平行线分线段成比例定理,易证得ME=DN=
| 1 |
| 3 |
解答:解:(1)PM=PN=BM.
证明:过点M作ME∥AC,
∵BA=BC,BD是△ABC的中线,
∴BD⊥AB,∠ABD=∠CBD,
∴BD⊥ME,
∵MN∥BC,
∴∠CBD=∠MPB,
∴∠ABD=∠MPB,
∴PM=BM;
∴BE=PE=
PB,
∵BP=2PD,
即PD=
PB,
∴PD=PE,
在△PME和△PND中,
∴△PME≌△PND(AAS),
∴PM=PN.
∴PM=PN=BM.
(2)PM=PN.
证明:过点M作ME∥AC,
∴
=
,
∵MN∥BC,
∴
=
,
∵PB=2PD,
∴
=
,
∴DN:DC=1:3,
即CD=3DN,
∵BD是△ABC的中线,
∴AD=CD,
∴CN:AC=1:3,
∴
=
=
,
∴
=
=
,
即AD=3EM,
∴CD=3EM,
∴EM=DN,
∵ME∥AC,
∴∠PME=∠PND,
在△PEM和△PDN中,
,
∴△PEM≌△PDN(AAS),
∴PM=PN.
证明:过点M作ME∥AC,
∵BA=BC,BD是△ABC的中线,
∴BD⊥AB,∠ABD=∠CBD,
∴BD⊥ME,
∵MN∥BC,
∴∠CBD=∠MPB,
∴∠ABD=∠MPB,
∴PM=BM;
∴BE=PE=
| 1 |
| 2 |
∵BP=2PD,
即PD=
| 1 |
| 2 |
∴PD=PE,

在△PME和△PND中,
|
∴△PME≌△PND(AAS),
∴PM=PN.
∴PM=PN=BM.
(2)PM=PN.
证明:过点M作ME∥AC,
∴
| ME |
| AD |
| BM |
| BA |
∵MN∥BC,
∴
| DN |
| DC |
| PD |
| DB |
∵PB=2PD,
∴
| PD |
| DB |
| 1 |
| 3 |
∴DN:DC=1:3,
即CD=3DN,
∵BD是△ABC的中线,
∴AD=CD,
∴CN:AC=1:3,
∴
| BM |
| BA |
| CN |
| CA |
| 1 |
| 3 |
∴
| EM |
| AD |
| BM |
| BA |
| 1 |
| 3 |
即AD=3EM,
∴CD=3EM,
∴EM=DN,
∵ME∥AC,
∴∠PME=∠PND,
在△PEM和△PDN中,
|
∴△PEM≌△PDN(AAS),
∴PM=PN.
点评:此题考查了平行线分线段成比例定理、全等三角形的判定与性质、等腰三角形的判定与性质以及平行线的性质等知识.此题综合性较强,难度较大,解题的关键是准确作出辅助线,利用数形结合思想求解.

练习册系列答案
相关题目
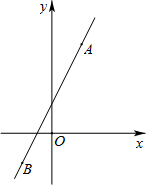 (2010•硚口区模拟)如图,已知直线y=kx+b经过A(1,3)、B(-1,-1)两点,求不等式kx+b>0的解集.
(2010•硚口区模拟)如图,已知直线y=kx+b经过A(1,3)、B(-1,-1)两点,求不等式kx+b>0的解集.
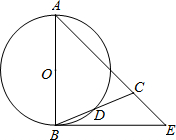 (2010•硚口区模拟)如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,E是AC的延长线上一点,连接BE,∠BEC+2∠CBE=90°.
(2010•硚口区模拟)如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于D点,E是AC的延长线上一点,连接BE,∠BEC+2∠CBE=90°.