题目内容
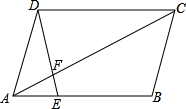平行四边形ABCD中，如果S△AEF=10cm2，AE：EB=1：3，求△AEF与△CDF的周长的比和S△CDF的面积．
解：∵AE：EB=1：3
∴AE：AB=1：4
∵四边形ABCD是平行四边形
∴AB∥CD
∴∠DCF=∠EAF，∠CDF=∠AEF
∴△AEF∽△CDF
∴AE：CD=AE：AB=1：4
∴△AEF与△CDF的周长的比为：1：4
△AEF与△CDF的面积的比为：1：16
∵S△AEF=10cm2
∴S△CDF=160cm2．
分析：由AE：EB=1：3可求得AE与AB的比值，再根据平行四边形的性质得到∠DCF=∠EAF，∠CDF=∠AEF，从而可得到△AEF∽△CDF，从而不难求得其相似比，根据相似三角形的周长比等于相似，面积比等于相似比的平方即可求得△AEF与△CDF的周长的比和S△CDF的面积．
点评：此题主要考查学生对平行四边形的性质及相似三角形的判定与性质的综合运用能力．
∴AE：AB=1：4
∵四边形ABCD是平行四边形
∴AB∥CD
∴∠DCF=∠EAF，∠CDF=∠AEF
∴△AEF∽△CDF
∴AE：CD=AE：AB=1：4
∴△AEF与△CDF的周长的比为：1：4
△AEF与△CDF的面积的比为：1：16
∵S△AEF=10cm2
∴S△CDF=160cm2．
分析：由AE：EB=1：3可求得AE与AB的比值，再根据平行四边形的性质得到∠DCF=∠EAF，∠CDF=∠AEF，从而可得到△AEF∽△CDF，从而不难求得其相似比，根据相似三角形的周长比等于相似，面积比等于相似比的平方即可求得△AEF与△CDF的周长的比和S△CDF的面积．
点评：此题主要考查学生对平行四边形的性质及相似三角形的判定与性质的综合运用能力．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
如图，在平行四边形ABCD中，高h=4，则平行四边形ABCD的面积S=
如图，在平行四边形ABCD中，AE：EB=1：2，S△AEF=3，则S△FCD=
如图，在平行四边形ABCD中，E是BD上一点，AE的延长线交DC于点F，交BC的延长线于点G．求证：
如图，在平行四边形ABCD中，E、F分别是AD、BC的中点，AC分别交BE、DF于G、H，下列结论：
如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE=∠B．