题目内容
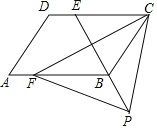
【题目】如图，已知抛物线
交
轴于点
、点
，交
轴于点C，且S△ABC=6.
（1）求
两点的坐标；
（2）求△ABC的外接圆与抛物线的对称轴的交点坐标；
（3）点E为抛物线上的一动点（点
异于
，且
在对称轴右侧），直线
交对称轴于N，
直线BE交对称轴于
，对称轴交
轴于
，试确定
、
的数量关系并说明理由.
【答案】（1）
；（2）
和
；（3）
与
的数量关系为
（
在
轴下方）或
（
在
轴上方）
【解析】试题分析：（1）设
， 
，根据题意和已知条件可得
， 
，解得
， 
，即可得
两点的坐标；（2））设
外接圆心为
， 
交对称轴于
，设对称轴交
轴于
，作
对称轴于
，可得
，从而求得点D的坐标，根据勾股定理求得半径的长，即可得△ABC的外接圆与抛物线的对称轴的交点坐标；（3）分
在
轴下方和
在
轴上方两种情况求
、
的数量关系.
试题解析：
（1）
， 
， 
， 
设
， 
， 
， 
，
， 
， 
（2）设
外接圆心为
， 
交对称轴于
， 
在直线
上，设对称轴交
轴于
，作
对称轴于
， 
， 
， 
， 
（3）
， 
， 
设
的解析式为
， 
， 
， 
设
的解析式为
， 
， 
， 
， 
即
即
①若
在
轴下方，则
， 
②若
在
轴上方，则
， 
与
的数量关系为
（
在
轴下方）或
（
在
轴上方）
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
