题目内容
若△ABC∽△A'B'C'，且S△ABC：S△A'B'C'=9：25，△ABC的周长为36，则△A'B'C'的周长为（ ）
A、
| ||
B、
| ||
| C、60 | ||
| D、100 |
分析：由△ABC∽△A′B′C′，且S△ABC：S△A'B'C′=9：25，根据相似三角形的面积比等于相似比的平方，即可求得其相似比，又由相似三角形的周长比等于相似比，即可求得△A′B′C′的周长．
解答：解：∵△ABC∽△A′B′C′，且S△ABC：S△A'B'C′=9：25，
∴△ABC与△A′B′C′的相似比为：3：5，
∵△ABC的周长与△A′B′C′的周长的比等于相似比，△ABC的周长为36，
∴
=
，
∴△A′B′C′的周长为60．
故选C．
∴△ABC与△A′B′C′的相似比为：3：5，
∵△ABC的周长与△A′B′C′的周长的比等于相似比，△ABC的周长为36，
∴
| 36 |
| △A′B′C′的周长 |
| 3 |
| 5 |
∴△A′B′C′的周长为60．
故选C．
点评：此题考查了相似三角形的性质．注意掌握相似三角形的面积比等于相似比的平方与相似三角形的周长比等于相似比是解此题的关键．
练习册系列答案
相关题目
7、如图，D是线段AB，BC的垂直平分线的交点，若∠ABC=50°，则∠ADC的大小是（ ）
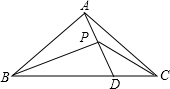如图，在等腰直角三角形ABC中，∠BAC=90°，在BC上截取BD=BA，作∠ABC的平分线与AD相交于点P，连结PC，若△ABC的面积为4cm2，则△BPC的面积为（ ）| A、4cm2 | B、3cm2 | C、2cm2 | D、8cm2 |