题目内容
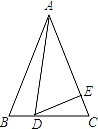
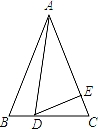
如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.
(1)求证: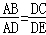 ;
;
(2)求线段EC的长度.
【考点】相似三角形的判定与性质.
【分析】(1)由条件可得到∠BAD=∠EDC,可证明△ABD∽△DCE,即可得到结论;
(2)由相似三角形的性质可得到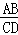 =
=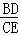 ,代入可求得EC.
,代入可求得EC.
【解答】解:(1)∵AB=AC,
∴∠B=∠C,
∵∠ADC是△ABD的一个外角,
∴∠ACD=∠B+∠BAD=∠ADE+∠EDC,
又∵∠B=∠ADE,
∴∠BAD=∠EDC,
∴△ABD∽△DCE,
∴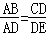 ;
;
(2)∵△ABD∽△DCE,
∴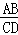 =
=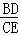 ,
,
∵BC=6,BD=2,
∴CD=4,
∴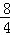 =
=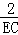 ,
,
解得EC=1.
【点评】本题主要考查相似三角形的判定和性质,由条件得到∠BAD=∠DCE证得△ABD∽△DCE是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
 •
• ,其中x=6.
,其中x=6.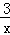 的图象上的两点,若x1<0<x2,则下列结论正确的是( )
的图象上的两点,若x1<0<x2,则下列结论正确的是( ) 在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是 .
在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是 .
 ,那么x的值是( )
,那么x的值是( ) B.
B. C.
C. D.
D.
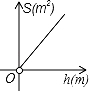 B.
B.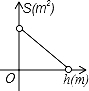 C.
C.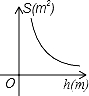 D.
D.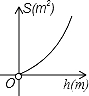
 ,求GC的长.
,求GC的长.