题目内容
(1)解不等式组:
,并把解集在数轴上表示出来.
(2)先化简,再求值:已知x=
+1,求(
-
)÷
的值.
|
(2)先化简,再求值:已知x=
| 2 |
| x+1 |
| x2-x |
| x |
| x2-2x+1 |
| 1 |
| x |
分析:(1)首先分别解出两个不等式的解集,再根据:解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到,即可得到不等式组的解集;
(2)首先把分式中得分子分母分解因式,然后通分约分,最后代入x的值即可.
(2)首先把分式中得分子分母分解因式,然后通分约分,最后代入x的值即可.
解答:解:(1)
,
由(1)得:x>-1,
由(2)得:x≤4,
所以原不等式组的解集为:-1<x≤4,
在数轴上的表示如下:
 ;
;
(2)当x=
+1时,
|
由(1)得:x>-1,
由(2)得:x≤4,
所以原不等式组的解集为:-1<x≤4,
在数轴上的表示如下:
 ;
;(2)当x=
| 2 |
|
点评:此题主要考查了不等式组的解法,分式的化简求值,解不等式组时,关键是把握准不等式组解集的准确找法.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
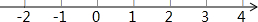
 (1)计算:4cos45°+(π+3)0-
(1)计算:4cos45°+(π+3)0-