题目内容
如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为 .


3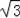
 .
.
【考点】旋转的性质;等边三角形的判定与性质.
【专题】几何图形问题.
【分析】首先,利用等边三角形的性质求得AD=3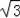
 ;然后根据旋转的性质、等边三角形的性质推知△ADE为等边三角形,则DE=AD.
;然后根据旋转的性质、等边三角形的性质推知△ADE为等边三角形,则DE=AD.
【解答】解:如图,∵在等边△ABC中,∠B=60°,AB=6,D是BC的中点,
∴AD⊥BD,∠BAD=∠CAD=30°,
∴AD=ABcos30°=6×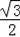
 =3
=3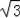
 .
.
根据旋转的性质知,∠EAC=∠DAB=30°,AD=AE,
∴∠DAE=∠EAC+∠CAD=60°,
∴△ADE的等边三角形,
∴DE=AD=3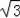
 ,
,
即线段DE的长度为3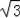
 .
.
故答案为:3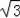
 .
.
【点评】本题考查了旋转的性质、等边三角形的性质.旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.

练习册系列答案
相关题目

 B.
B.
 C.
C. D.
D.