题目内容
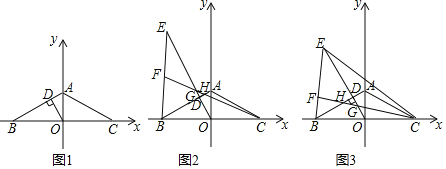
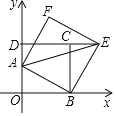
【题目】如图,矩形OBCD位于直角坐标系中,点B(![]() ,0),点D(0,m)在y轴正半轴上,点A(0,1),BE⊥AB,交DC的延长线于点E,以AB,BE为边作ABEF,连结AE.
,0),点D(0,m)在y轴正半轴上,点A(0,1),BE⊥AB,交DC的延长线于点E,以AB,BE为边作ABEF,连结AE.
(1)当m=![]() 时,求证:四边形ABEF是正方形.
时,求证:四边形ABEF是正方形.
(2)记四边形ABEF的面积为S,求S关于m的函数关系式.
(3)若AE的中点G恰好落在矩形OBCD的边上,直接写出此时点F的坐标.
【答案】(1)证明见解析;(2)S=![]() m(m>0);(3)满足条件的F坐标为(
m(m>0);(3)满足条件的F坐标为(![]() ,2)或(
,2)或(![]() ,4).
,4).
【解析】
(1)只要证明△ABO≌△CBE,可得AB=BE,即可解决问题;
(2)在Rt△AOB中利用勾股定理求出AB,证明△ABO∽△CBE,利用相似三角形的性质求出BE即可解决问题;
(3)分两种情形I.当点A与D重合时,II.当点G在BC边上时,画出图形分别利用直角三角形和等边三角形求解即可.
解:(1)如图1中,

∵m=![]() ,B(
,B(![]() ,0),
,0),
∴D(0,![]() ),
),
∴OD=OB=![]() ,
,
∴矩形OBCD是正方形,
∴BO=BC,
∵∠OBC=∠ABE=90°,
∴∠ABO=∠CBE,∵∠BOA=∠BCE=90°,
∴△ABO≌△CBE,
∴AB=BE,
∵四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∵∠ABE=90°,
∴四边形ABEF是正方形.
(2)如图1中,
在Rt△AOB中,∵OA=1,OB=![]() ,
,
∴AB=![]() =2,
=2,
∵∠OBC=∠ABE=90°,
∴∠OBA=∠CBE,
∵∠BOA=∠BCE=90°,
∴△ABO∽△CBE,
∴![]() ,
,
∴![]() ,
,
∴BE=![]() m,
m,
∴S=ABBE=![]() m(m>0).
m(m>0).
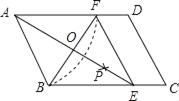
(3)①如图2中,当点A与D重合时,点G在矩形OBCD的边CD上.

∵tan∠ABO=![]() ,
,
∴∠ABO=30°,
在Rt△ABE中,∠BAE=∠ABO=30°,AB=2,
∴AE=![]() ,
,
∵AG=GE,
∴AG=![]() ,
,
∴G(![]() ,1),设F(m,n),
,1),设F(m,n),
则有![]() ,
,![]() ,
,
∴m=![]() ,n=2,
,n=2,
∴F(![]() ,2).
,2).
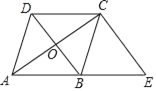
②如图3中,当点G在BC边上时,作GM⊥AB于M.

∵四边形ABEF是矩形,
∴GB=GA,
∵∠GBO=90°,∠ABO=30°,
∴∠ABG=60°,
∴△ABG是等边三角形,
∴BG=AB=2,
∵FG=BG,
∴F(![]() ,4),
,4),
综上所述,满足条件的F坐标为(![]() ,2)或(
,2)或(![]() ,4).
,4).

 53随堂测系列答案
53随堂测系列答案