题目内容
抛物线y=(x-2)2+m经过点(1,
),则下列各点在抛物线上的是( )
| 3 |
| 2 |
| A、(0,1) | ||||
B、(
| ||||
C、(3,
| ||||
D、(-1,
|
考点:二次函数图象上点的坐标特征
专题:计算题
分析:先把点(1,
)代入y=(x-2)2+m求出m得到抛物线的解析式为y=(x-2)2+
,然后把x=0,
,3,-1代入抛物线解析式进行出对应的函数值,再判断点是否在抛物线上.
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:把(1,
)代入y=(x-2)2+m得(1-2)2+m=
,解得m=
,
所以抛物线的解析式为y=(x-2)2+
,
当x=0时,y=(0-2)2+
=
;当x=
时,y=(
-2)2+
=
;当x=3时,y=(3-2)2+
=
;当x=-1时,y=(-1-2)2+
=
,
所以点(3,
)在抛物线y=(x-2)2+
上.
故选C.
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
所以抛物线的解析式为y=(x-2)2+
| 1 |
| 2 |
当x=0时,y=(0-2)2+
| 1 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 11 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 19 |
| 2 |
所以点(3,
| 3 |
| 2 |
| 3 |
| 2 |
故选C.
点评:本题考查了二次函数图象上点的坐标特征:二次函数y=ax2+bx+c(a≠0)的图象上点的坐标满足其解析式.

练习册系列答案
相关题目
一元二次方程x(x-3)=0的根的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、只有一个实数根 |
| D、没有实数根 |
下列四位同学的说法中,正确的是( )
| A、墨墨说:0除以任何一个不等于0的数都得0 | ||
| B、亮亮说:任何数除以0都得0 | ||
C、茗茗说:除以-
| ||
| D、丽丽说:两数相除所得的商就是这两个数的绝对值相除所得的商 |
 请利用直尺和圆规,过定点A作⊙O的切线,不写作法,保留尺规作图的痕迹.
请利用直尺和圆规,过定点A作⊙O的切线,不写作法,保留尺规作图的痕迹.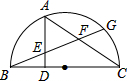 如图,BC是半圆O的直径,点G是半圆上任意一点,点A为
如图,BC是半圆O的直径,点G是半圆上任意一点,点A为
 如图,在△ABC中,AB=AC,D为AC上一点,且AD=BD=BC.
如图,在△ABC中,AB=AC,D为AC上一点,且AD=BD=BC.